Hipotesis Statistik merupakan salah satu langkah yang dipakai dalam sebuah penelitian. Biasanya setelah dilakukan penetapan dugaan sementara pada tema riset, akan dilanjutkan dengan uji hipotesis statistik yang akan berhubungan dengan kesimpulan dari sebuah penelitian yang bersifat kuantitatif.
Pengujian akan dilakukan untuk memperkuat dugaan sementara, dimana nantinya hasilnya akan dibandingkan dengan fakta yang ada. Kalau hasilnya terbukti benar, maka nantinya hipotesis bisa dipakai, tapi kalau ternyata salah maka dapat pula ditolak atau dilakukan penyangkalan.
Beda Hipotesis Penelitian dengan Hipotesis Statistik

Meskipun sama-sama hipotesis, namun ternyata ada perbedaan signifikan antara hipotesis penelitian dengan statistik.
Cara Pembuktian
Untuk cara membuktikan hipotesis penelitian, harus melibatkan semua yang menjadi objek penelitian. Misalnya, ada dugaan sementara bahwa di SMP A semua siswanya memiliki ponsel Android. Maka hipotesis penelitian yang dilakukan harus melibatkan semua siswa, dimana mereka harus didata kepemilikan HP nya.
Kalau ternyata berdasarkan hasil penelitian tidak semua siswa memakai HP Android, maka dugaan sementara bisa ditolak.
Sedangkan untuk hipotesis statistik, untuk menentukan benar atau salahnya dibuktikan hanya dengan mengambil sampel yang kemudian nantinya diuji dengan cara tertentu.
Lalu untuk contoh uji hipotesis ini yaitu, ada dugaan bahwa warga desa Z kebanyakan adalah PNS. Kemudian peneliti akan mengambil sampel dari warga desa dengan rumus tertentu, untuk memastikan apakah dugaan itu benar atau tidak.
Kapan Digunakan
Hipotesis penelitian dilakukan untuk berbagai jenis penelitian, terutama yang bersifat kualitatif. Sementara untuk hipotesis statistik kebanyakan akan dipakai pada riset kuantitatif.
Bagaimana Cara Melakukan Uji Hipotesis Statistik
Ada lima cara bisa digunakan untuk melakukan uji hipotesis statistik, untuk melihat apakah sebuah dugaan sementara itu benar atau salah. Para peneliti wajib paham cara tersebut, sebelum menggunakannya pada sebuah riset ilmiah.
Melakukan Perumusan Hipotesis
Cara pertama adalah dengan merumuskan sebuah hipotesis atau dugaan sementara. Gunanya adalah untuk menegaskan batasan dari riset yang akan dilakukan. Pada proses perumusan ini, ada dua jenis dari dugaan sementara yang biasa digunakan.
H0
Biasa dibaca H nol, yaitu perumusan untuk hipotesis yang ditolak
Contoh dari H0 ini adalah: Tidak ada hubungannya antara jam tidur siswa dengan kemampuannya di sekolah.
H1
Biasa dibaca H satu atau disebut juga H alternatif, akan berfungsi untuk menegaskan sebuah hipotesis yang diterima atau sesuai dengan dugaan sementara
Contoh dari H1 ini adalah: ada hubungan antara waktu seseorang duduk dengan kesehatan pinggangnya
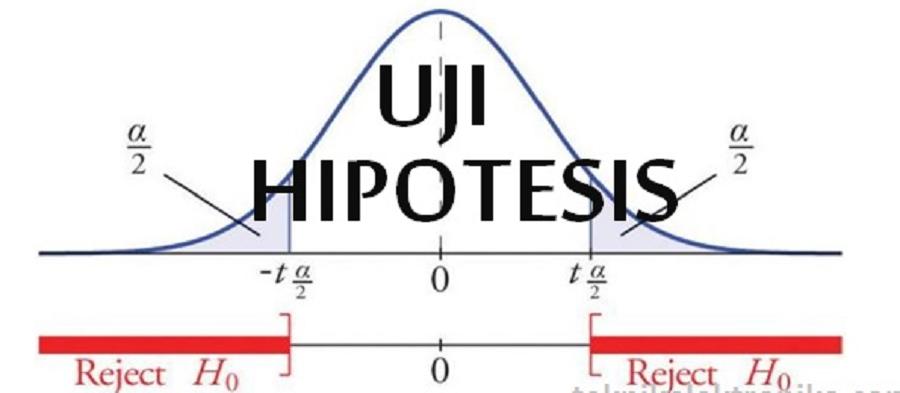
Menentukan Taraf Nyata
Apa itu taraf nyata? Biasa juga disebut dengan batas dari toleransi kesalahan dari sebuah dugaan, batas ini menggunakan persentase dalam penentuannya. Biasanya, taraf nyata dari sebuah hipotesis ini ada yang nilainya 1 persen, lima persen, hingga 10 persen.
Dalam realisasi penggunaan taraf nyata ini menggunakan simbol ɑ, untuk mempermudah saat menjelaskan batas yang ingin ditetapkan
Menentukan Apa Saja Kriteria Uji
Kriteria uji dibuat untuk memutuskan apakah dugaan sementara itu ditolak atau diterima. Untuk H0, nantinya nilai uji akan ada di luar dari nilai yang sudah ditetapkan. Sedangkan untuk H1, nilainya ada di dalam rentang nilai yang ditetapkan.
Menetapkan Nilai dari Uji Statistik
Saatnya untuk melakukan uji hipotesis statistik, sehingga nantinya bisa didapat sebuah hasil yang diinginkan. Apakah H0 atau H1.
Bagaimana cara menetapkan nilai tersebut? ada rumus uji hipotesis yang digunakan. Rumus tersebut sudah baku dan memang sudah digunakan dalam berbagai penelitian. Apa rumusnya?
Z = x̄n – µ0
σ√n
z = statistik yang menjadi objek pengujian
x̄n = rata rata dari sampel
µ0 = hipotesis jenis nol, disebut juga dengan nilai mean objek yang diuji
σ = deviasi standar
n = jumlah objek atau sampel yang diuji
Menetapkan Kesimpulan
Cara ini adalah yang terakhir setelah semua yang sebelumnya dilakukan. Penentuan kesimpulan akan sangat berhubungan dengan hasil uji hipotesis.
Contoh Hipotesis Statistik
Selanjutnya, dalam penggunaannya Ada beberapa contoh dari hipotesis statistik. Tiga diantaranya sangat penting diketahui karena sangat berhubungan dengan sebuah penelitian yang sering dilakukan.
Komparatif atau Perbedaan
Membandingkan kondisi tertentu yang berhubungan dengan riset. Contohnya, ada perbedaan kecerdasan anak yang ikut les dan tidak ikut les.
Kausalitas atau Sebab Akibat
Hipotesis sebab akibat berhubungan dengan koneksi variabel yang akan menyatakan sebab akibat. Seperti:
H0: β = 0
H1: β ≠ 0
Untuk dugaan: adanya hubungan antara jumlah karyawan dengan kesuksesan sebuah bisnis. Hipotesisnya jika H0 ditolak, maka pengaruhnya akan ada dua yaitu positif atau negatif.
Asosiatif atau Berhubungan Korelasional
Berhubungan dengan dua variabel yang diteliti, dimana keduanya memiliki korelasi atau keterkaitan. Contohnya adalah:
Dugaan sementara: terdapat korelasi atau hubungan antara nilai mahasiswa dengan absensi kehadiran dengan taraf nyatanya:
H0: p ≤ 0
H1: p ˃ 0
Hasil uji hipotesisnya ternyata: ada hubungan antara nilai mahasiswa dengan absensi kehadiran, dimana semakin sering mahasiswa hadir maka nilainya lebih baik
Bagaimana Ciri Ciri dari Sebuah Hipotesis Statistik yang Bagus
Walaupun hanya berupa dugaan sementara H0 dan H1, namun ternyata tidak semua hipotesis statistik itu bagus dan bisa dipakai dalam sebuah penelitian. Jika Anda mau menggunakan yang bagus dan tepat, maka pastikan hipotesis itu memiliki ciri seperti berikut:
- Sebuah hipotesis itu harus bisa diuji kelayakannya menggunakan rumus uji hipotesis statistik seperti yang sudah dijelaskan sebelumnya
- Sebuah hipotesis itu juga harus sesuai dengan sebuah fakta yang menjadi bagian dari penelitian. Sebagai landasan yang tepat dan nantinya bisa dipertanggungjawabkan
- Sebuah hipotesis akan dikatakan baik kalau dapat menjelaskan sebuah fakta dengan tepat, baik itu kebenaran dari fakta atau malah sebaliknya
- Sebuah hipotesis tidak boleh rumit, melainkan sederhana agar mudah dipahami oleh peneliti maupun siapa saja yang membaca penelitian tersebut
- Sebuah hipotesis harus sesuai dengan ilmu sebagai landasan penentuan dugaan sementara tersebut.
Apa Pentingnya Menggunakan Hipotesis Statistik?
Sebagian besar peneliti pastinya sudah paham kalau hipotesis statistik itu penting dipakai, terutama pada beberapa jenis penelitian karena beberapa hal di bawah ini.
Awareness untuk Peneliti
Hipotesis ini akan menjadi salah satu awareness bagi peneliti, supaya mereka bisa mengetahui kondisi dari suatu fakta yang mungkin saja sebelumnya tidak diperhatikan.
Panduan Penting Penelitian
Penelitian tanpa hipotesis tidak akan sempurna karena dugaan sementara ini akan menjadi sebuah panduan dalam pengujian menggunakan rumus. Alhasil nantinya bisa didapatkan hasil yang sesuai baik itu antarfakta yang digunakan maupun dengan fakta yang tersedia.
Mempertegas Batasan
Peneliti menjadi punya batasan ruang lingkup penelitian, yang mengacu pada dugaan sementara. Nantinya peneliti akan lebih terarah dan fokus melakukan tahapan penelitian
Lebih Fokus dalam Penggunaan Fakta
Jika banyak fakta yang dipakai, maka dengan hipotesis akan membantu membuat peneliti fokus pada berbagai fakta tersebut
Apakah Anda sudah paham seberapa pentingnya uji hipotesis statistik? Dengan berbagai penjelasan di atas setidaknya bisa menjadi referensi untuk melakukan sebuah penelitian yang sesuai dengan tujuan awalnya.