Belajar konversi sistem bilangan memang tak mudah, oleh karena itu Anda perlu mengasah kemampuan dalam mengkonversi bilangan dengan bantuan latihan-latihan mengerjakan beberapa contoh soal. Berikut ini kami memfasilitasi beberapa contoh soal yang dapat Anda jadikan acuan dalam belajar konversi sistem bilangan.
1. Berapakah nilai desimal dari bilangan biner berikut 1101 0010(2) = ….. (10)?
Jawab: 1101 0010(2) = = (1 x 27) + (1 x 26) + (0 x 25) + (1 x 24) + (0 x 23) + (0 x 22) + (1 x 21) + (0 x 20) = 128 + 64 + 0 + 16 + 0 + 0 + 2 + 0 = 210(10)
2. Berapakah nilai desimal dari bilangan biner berikut 1111(2) = ….. (10)?
Jawab: 1111(2) = (1 x 23) + (1 x 22) + (1 x 21) + (1 x 20) = 8 + 4 + 2 + 1 = 15(10)
3. Berapakah nilai Biner dari bilangan desimal berikut 60(10) = ….. (2)?
Jawab:

Jadi hasil dari 60(10) = 111100(2)
4. Berapakah nilai desimal dari bilangan oktal 129(8) = …… (10)
Jawab: 129(8) = (1 x 82) + (2 x 81) + (9 x 80) = 64 + 16 + 9 = 89(10)
5. Berapakah nilai oktal dari bilangan desimal 84(10) = ….. (8)
Jawab:

Jadi bilangan oktal dari 87(10) = 124(8)
6. Berapakah nilai heksadesimal dari bilangan desimal 8026(10) = ….. (16)
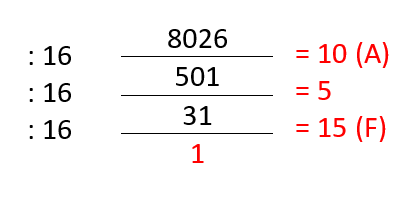
Jadi bilangan heksadesimal dari 8026(10) = 1F5A(16)
7. Berapakah nilai desimal dari bilangan heksadesimal 125A(16) = …… (10)
Jawab: 125A(16) = (1 x 163) + (2 x 162) + (5 x 161) + (10 x 160) = 4096 + 512 + 80 + 10 = 4698(10)
8. Berapakah nilai oktal dari bilangan biner 100111(2) = …… (8)
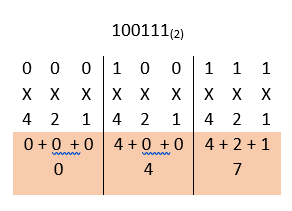
Jadi nilai oktal dari bilangan biner 110111(2) = 047(8).
9. Berapakah bilangan heksadesimal dari bilangan biner 1011 1110(2) …… (16)
Jawaban:
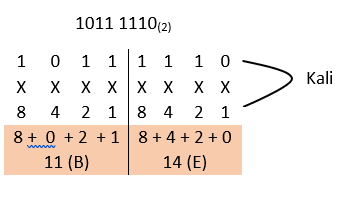
Jadi nilai heksadesimal dari 1011 1110(2) = BE(16)
10. Berapakah bilangan heksadesimal dari bilangan oktal berikut 272(8) = …..(16)
Jawaban: ikuti langkah-langkah berikut ini
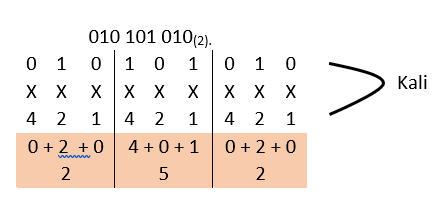
A. Pisahkan bilangan 272 menjadi tiga bagian yaitu 2,7, dan 2. Kemudian lakukan konversi menjadi bilangan biner.
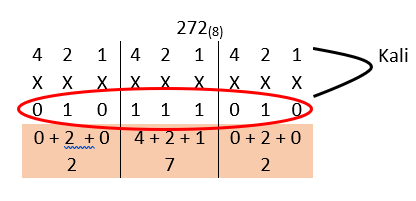
Jadi nilai biner dari bilangan 272(8) = 010 111 010(2)
B. Setelah diperoleh bilangan biner 010 111 010(2), barulah lakukan konversi dari biner ke heksadesimal. Dengan membaginya di tiap bagian terdiri dari 4 digit, 0000 1011 1010(2).
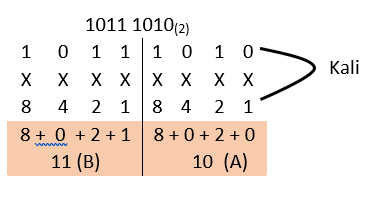
Jadi nilai heksadesimal dari 1011 1010(2) = BA(16)
11. Berapakah nilai oktal dari bilangan heksadesimal berikut AA(16) = …..(8)
Jawaban: ikuti langkah-langkah berikut
1. Pisahkan bilangan heksadesimal AA menjadi dua bagian yaitu A dan A. Kemudian lakukan konversi menjadi bilangan biner.
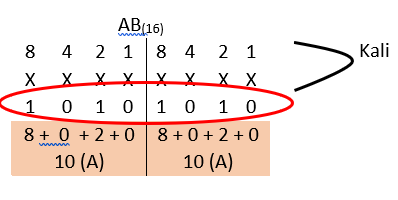
Jadi nilai dari AA(16) = 1010 1010(2)
B. Setelah diperoleh bilangan biner 1010 1010(2), barulah lakukan konversi dari biner ke oktal. Dengan membaginya menjadi tiga bagian dimana di tiap bagian terdiri dari 3 digit, 010 101 010(2).
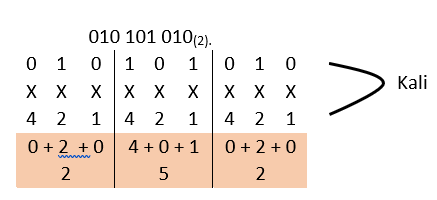
Jadi nilai oktal dari bilangan 010 101 010(2)= 252(8)
12. Hitunglah penjumlahan bilangan biner 1110(2) + 0101(2)?
Jawaban:

Jadi hasil perhitungan dari 1110(2) + 0101(2) = 10011(2)
13. Hitunglah pengurangan bilangan biner 1111(2) – 1101(2)?
Jawaban:

Jadi hasil perhitungan dari 1111(2) – 1101(2) = 0010(2)
Sekian beberapa contoh soal mengenai sistem bilangan, semoga bermanfaat dan menambah ilmu bagi Anda yang membacanya. Sampai jumpa kembali 😊