Z score adalah suatu ukuran penyimpangan data dari nilai rata-rata yang telah diukur dengan satuan standar deviasinya. Jika nilai yang diperoleh diatas rata-rata maka Z score-nya akan bernilai positif, sedangkan jika nilai yang diperoleh dibawah rata-rata maka Z score-nya bernilai negatif. Z score juga memiliki sebutan lain yaitu nilai standar atau nilai baku.
Proses standarisasi nilai-nilai skor mentah atau nilai yang diamati dari distribusi normal menjadi Z score memiliki manfaat untuk memungkinkan Anda menghitung probabilitas skor yang terjadi dalam distribusi normal dan memungkinkan Anda untuk membandingkan dua skor yang berasal dari populasi berbeda.
Penting untuk diketahui bahwa Z score hanya bermanfaat atau bermakna jika dilakukan untuk pengamatan yang berbentuk distribusi normal. Distribusi normal standar yang dimaksud adalah distribusi yang berbentuk normal dengan nilai rata-ratanya adalah nol dan nilai standar deviasinya adalah satu.
Pengertian Z Score
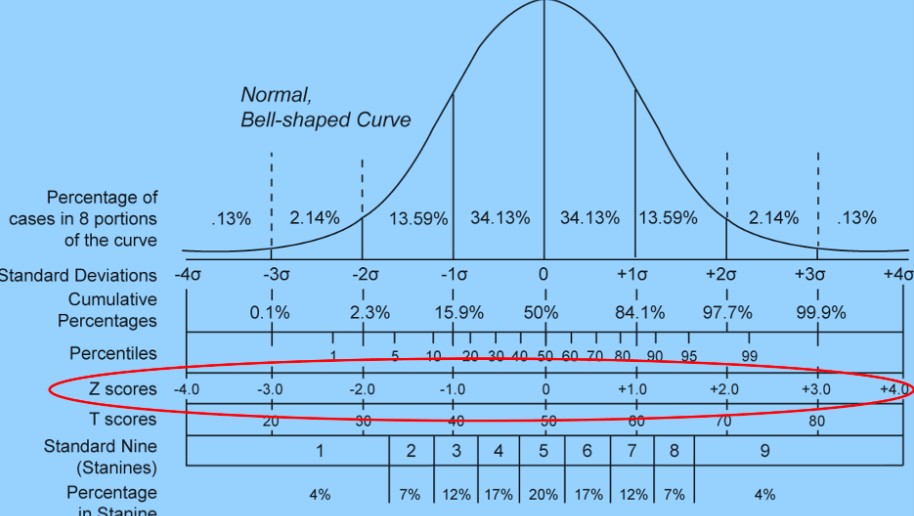
Z score menjadi salah satu konsep bilangan yang banyak digunakan dalam ilmu statistika dan keuangan. Z score merupakan konsep perhitungan yang menunjukkan besarnya nilai suatu sampel terhadap rat-rata dalam satuan standar deviasi.
Z score terletak pada suatu titik di sumbu datar kurva normal. Z score dapat berbentuk positif maupun negatif, nilai positif artinya skor yang diperoleh di atas rata-rata sementara nilai negatif artinya skor yang diperoleh di bawah rata-rata. Z score memiliki manfaat dalam berbagai bidang kehidupan, khususnya bagi statistikawan dan pedagang.
Konsep dari z score biasanya dipakai untuk mengadaptasi skor dari variasi data set yang membuat skor-skor tersebut dapat dikomparasi ke data lainnya secara akurat.
Rumus Z Score
Z score dapat diterapkan pada dua ranah yaitu statistika dan finansial. Berikut adalah penjelasannya:
Rumus Z-Score Altman
Dalam dunia finansial, Z score memiliki sebutan sebagai altman Z score. Z score ini dapat menghitung variabilitas pengamatan dan dapat digunakan untuk pebisnis dalam menentukan nilai volatilitas pasar. Berikut adalah rumus dari Z score altman:
![]()
Keterangan:
- Z (Zeta) = Z score Altman
- A = Total aset (modal perusahaan)
- B = Pemasukan / saldo laba (total aset)
- C = Pendapatan sebelum bunga dan pajak atau EBIT (total aset)
- D = Nilai pasar ekuitas (nilai buku terhadap nilai liabilitas)
- E = Angka penjualan (total aset)
Selain itu, Z score bisa berguna untuk memprediksi kondisi tingkat kesulitan yang sedang dihadapi oleh perusahaan. Dengan indikator angka Z score dibawah 1,8 berarti perusahaan bangkrut, sedangkan perusahaan yang memiliki kondisi keuangan solid akan memiliki angka yang mendekati 3. Berikut adalah tabel interpretasi dari Z score altman:
| Z < 1,81 | 1,81 | Z > 2,99 |
| Zona distress (mendekati kebangkrutan) | Zona abu-abu | Zona aman |
Rumus Z Score Statistik
Dalam dunia statistik, Z score dijadikan acuan untuk mengetahui perbandingan antara nilai individu subjek terhadap simpangan baku. Z score diterapkan dalam kehidupan sehari-hari seperti dalam bidang kesehatan, ilmu fisika, ilmu sosial dan lainnya. Berikut adalah rumus dari Z score statistik:

Keterangan:
- Z = Nilai Z score
- X = Nilai subjek atau individu (skor yang akan diperiksa)
- X_ = Nilai rata-rata atau mean
- S = Standar deviasi atau simpangan baku
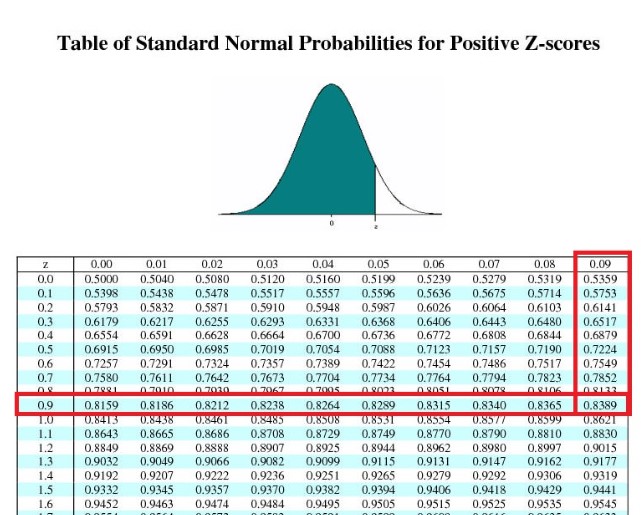
Untuk menginterpretasikan nilai z score, Anda dapat menggunakan tabel Z score untuk menentukannya. Jika angka dalam tabel z statistik adalah negatif maka posisinya akan berada di sisi sebelah kiri mean pada kurva normal, sementara jika positif maka posisinya akan berada di kanan mean pada kurva normal.
Cara Menghitung Z Score
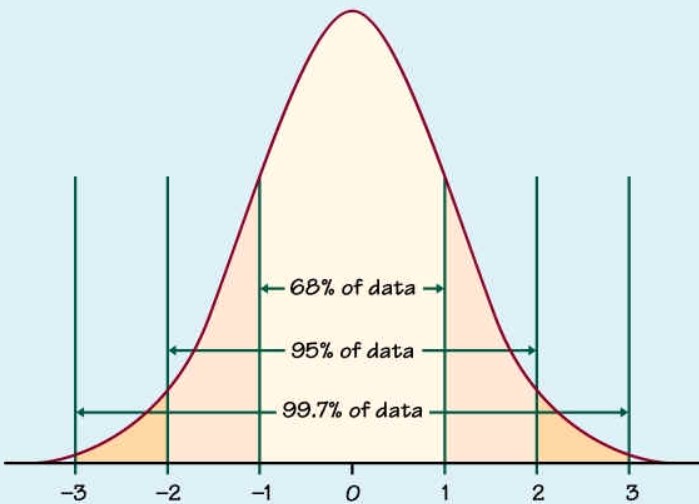
Ada berbagai cara yang dapat dilakukan untuk memperoleh nilai Z score, pada Z score altman caranya cukup sederhana hanya dengan menambahkan nilai dari A,B, C, D dan E. Sementara Z score dalam perhitungan statistik cukup rumit, berikut adalah pembahasan caranya satu persatu:
Menghitung Z Score Secara Manual Menggunakan Kalkulator
Untuk menghitung Z score data yang diperlukan adalah skor rata-rata dan juga standar deviasi, berikut adalah langkah-langkahnya:
- Kumpulkan data (data subjek dan data sampel yang akan dicari nilai Z skor-nya)
- Menghitung nilai rata-rata dengan cara menjumlahkan semua angka dalam data / sampel deng mengimbangi dengan jumlah data/sampel
- Menghitung varians (tingkat penyebaran rata-rata).
- Menghitung nilai standar deviasi
- Setelah semua data yang dibutuhkan terkumpul, proses selanjutnya adalah menghitung Z score dengan rumus

Menghitung Z Score dengan Ms. Excel
Menghitung secara manual dengan kalkulator bisa dilakukan jika datanya sedikit, akan tetapi Anda akan kewalahan jika data yang dihitung banyak. Oleh karena itu menggunakan bantuan Ms.Excel adalah jalan keluarnya. Berikut adalah langkah-langkahnya:
- Buka halaman baru pada Microsoft Excel
- Inputkan data-data yang akan dilakukan perhitungan
- Ketikan formula mean, dengan detail formula =AVERAGE(cell). Contohnya =AVERAGE(A1:A15)
- Ketikan formula standar deviasi, dengan detail formula =STDEV(cell). Contohnya =STDEV (B1:B15)
- Temukan nilai Z score pada titik data. Perlu diperhatikan cell titik data, inputkan cell kosong di bagian sebelah formulanya sebagai berikut =(datapoint – $mean)/$standarddeviation. Misalkan Anda ingin memperoleh Z score pada sel A1, maka tepat di sebelahnya (kolom B1) inputkan formula =(B1-$mean$)/$Standarddeviasi$
- Masukan formula Z score pada titik tabel lain dengan cara menarik kursor ke seluruh bagian kolom yang tersisa di tabel. Dengan begini Anda dapat menghitung Z score tanpa perlu memakan banyak waktu.
Menghitung Z score dengan SPSS
Jika ingin lebih praktis dan canggih, Anda dapat menggunakan bantuan dari aplikasi SPSS. Berikut adalah cara menghitung Z score dengan bantuan SPSS:
- Buka halaman baru pada aplikasi SPSS
- Siapkan data yang akan dihitung pada lembar SPSS
- Klik menu Analyze lalu pilih Descriptive Statistik dan klik icon Descriptive.
- Setelahnya kotak dialog akan muncul pada layar, pada saat itu Anda dapat memasukan variabel atau data subjek yang akan dicari nilai Z score-nya.
- Centang bagian checkbox yang terdapat tulisan save standardized values as variables.
- Tunggu beberapa saat untuk aplikasi memproses data, tidak sampai satu menit nilai Z score akan muncul otomatis di layar.
Contoh Kasus Perhitungan Z Score
Seorang siswa bernama isabel memperoleh nilai 80 pada mata pelajaran matematika, sedangkan nilai rata-rata dan standar deviasi seluruh siswa di kelas adalah 75 dan 9,29. Pada kelas yang sama, isabel memperoleh nilai 85 untuk mata pelajaran bahasa jepang, dengan nilai rata-rata seluruh siswa adalah 82,5 dan standar deviasi nya adalah 7,54. Pertanyaanya adalah pada mata pelajaran manakah isabel paling berprestasi?
Diketahui:
- Xmat = 80
- X_mat= 75
- Smat = 9,29
- Xjpn = 85
- X_jpn = 82,5
- Sjpn = 7,54
Ditanya Zmat dan Zjpn?
1. Z score pada mata pelajaran matematika
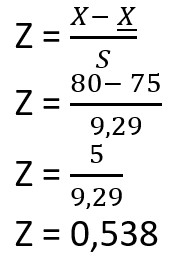
2. Z score pada mata pelajaran bahasa jepang
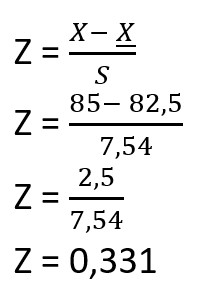
3. Dari hasil perhitungan diatas menunjukkan bahwa Z score pada mata pelajaran matematika (Zmat) lebih besar daripada Z score pada mata pelajaran bahasa jepang (Zjpn), itu berarti isabel lebih berprestasi pada mata pelajaran matematika dibandingkan dengan bahasa jepang.