Rumus diagram venn berguna untuk memudahkan pengguna dalam melakukan penyajian data diagram. Inilah yang menjadi jenis diagram gambar untuk menghubungkan satu kelompok objek yang mempunyai kesamaan.
Diagram venn memang seringkali digunakan sebagai penggambaran adanya fraksi, persimpangan atau perbandingan data. Selain itu, juga seringkali digunakan dalam menyajikan data yang berbentuk olahan data, statistik, matematika maupun hasil dari aplikasi komputer.
Apa itu Diagram Venn?
Diagram venn memiliki pengertian, metode untuk merepresentasikan hubungan antar objek melalui grafik diagram. Tujuannya supaya lebih akurat dalam menunjukkan hubungan yang terjadi pada anggota himpunan.
Himpunan dikorelasikan dalam sekelompok objek dengan kesamaan nilai atau jumlah frekuensi. Supaya lebih memahami mengenai diagram, maka Anda harus mengetahui himpunan terlebih dahulu.
Untuk himpunan itu sendiri menjadi aspek terpenting pada suatu diagram venn, karena tanpa adanya himpunan otomatis, diagram venn tersebut tidak dapat dibuat. Bisa dikatakan juga bahwa himpunan menjadi kumpulan objek yang bisa diartikan secara jelas yaitu jumlah maupun frekuensi data.
Proses pembuatan himpunan yang mudah dibaca, maka dianjurkan bagi Anda agar menggunakan tanda kurung. Dengan adanya simbol tanda kurung inilah, pembaca dapat mengetahui bahwa data yang terdapat di dalam kurung adalah data himpunan.
Karakteristik Diagram
Diagram venn lebih dikenal sebagai diagram Euler-Venn yang merupakan representasi sederhana berasal dari himpunan diagram penggambaran. Pada biasanya akan menggunakan persegi panjang yang berperan sebagai set universal maupun lingkaran pada set yang dipertimbangkan.
Tidak sampai di situ saja, fungsinya juga sangat beragam, karena diagram venn mempunyai karakteristik secara khusus seperti berikut ini:
- Daerah himpunan A dan B bisa ditulis menggunakan notasi A∩B.
- Diagram venn digunakan untuk pengelompokan jumlah anggota dari himpunan A saja.
- Diagram venn dapat digunakan untuk menghitung jumlah anggota dari himpunan B meskipun tidak menggunakan anggota himpunan A.
- Himpunan semesta mendeskripsikan seluruh data atau nilai yang ada.
- DI dalam himpunan semesta memiliki anggota himpunan yang bukan hanya dari bagian himpunan A atau himpunan B saja.
Rumus Diagram Venn
Rumus diagram Venn memang cukup beragam, karena hal ini tergantung dari jenis yang digunakan. Mengingat bahwa diagram venn itu sendiri terbagi menjadi beragam jenis.
Akan tetapi, secara umum diagram venn ini hanya memiliki tiga empat jenis yaitu himpunan berpotongan, himpunan bagian, himpunan saling lepas, dan himpunan sama. Oleh karena itu, rumus dari diagram venn juga berbeda. Berikut ini rumus yang dimaksud:
n(A∪B) = n (A) + n (B) – n (A∩ B)
n (A ∪ B ∪ C) = n (A) + n (B) + n (C) – n (A ∩ B) – n (B ∩ C) – n (C ∩ A) + n (A ∩ B ∩ C)
Keterangan:
n(X)= Jumlah elemen di himpunan X
n(A)= Jumlah elemen di himpunan A
X= Jumlah elemen dari himpunan A
Y= Jumlah elemen dari himpunan B
Z= Jumlah elemen dari himpunan A dan B untuk keduanya
W= Jumlah elemen tidak termasuk pada himpunan a atau himpunan b
Diagram venn dapat menunjukkan adanya kemungkinan hubungan hipotesis ataupun logika antar kelompok, baik itu set himpunan atau grup maupun benda ataupun objek. Ciri dari diagram venn yaitu memiliki banyak anggota semesta.
Akan tetapi, bukan bagian dari himpunan A atau B saja. Selain itu, juga mempunyai himpunan semesta yang menggambarkan nilai atau total data yang sedang dibicarakan.
Bentuk Diagram Venn
Berikut ini beberapa bentuk diagram venn yang bisa diketahui, yaitu:
1. Himpunan yang Sama
Untuk diagram venn akan menyatakan bahwa apabila himpunan A maupun B terdiri dari himpunan yang sama, otomatis bisa disimpulkan bahwa setiap anggota B adalah anggota A.
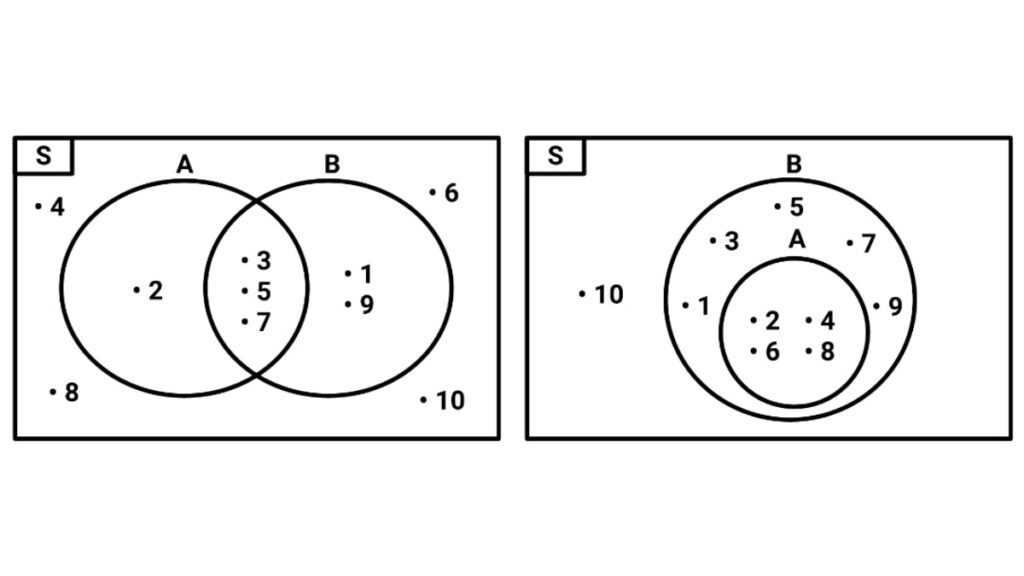
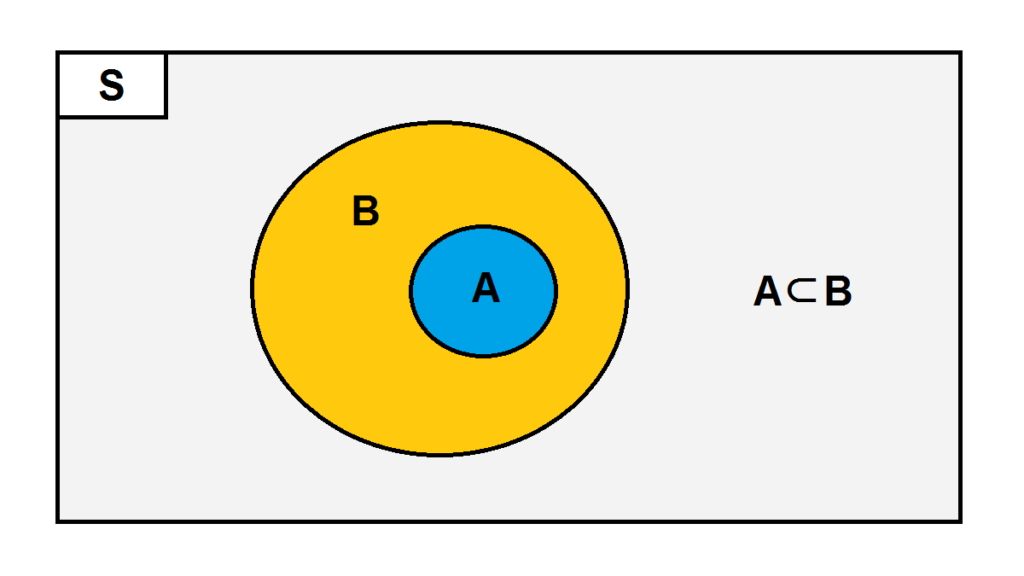
2. Himpunan Bagian
Himpunan bagian bisa dikatakan sebagian dari himpunan B jika seluruh anggota himpunan A adalah anggota dari himpunan B.
3. Himpunan Saling Lepas

Bisa dikatakan bahwa himpunan A dan himpunan B akan saling lepas apabila anggota dari himpunan A tidak ada yang memiliki anggota sama pada himpunan B. Sementara himpunan saling lepas bisa dituliskan menggunakan simbol A//B.
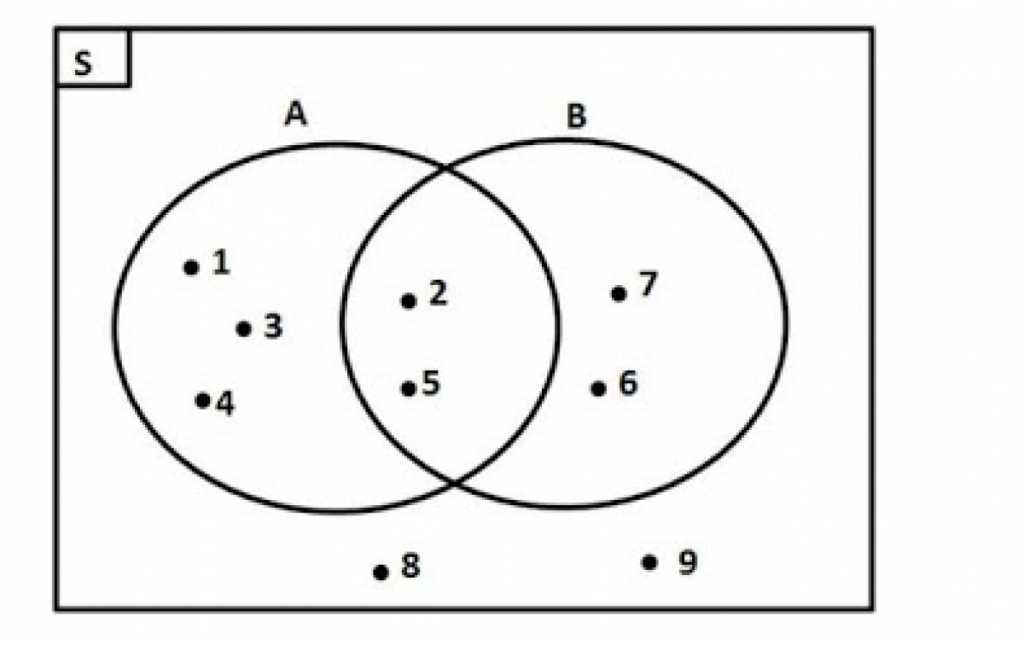
4. Himpunan Saling Berpotongan
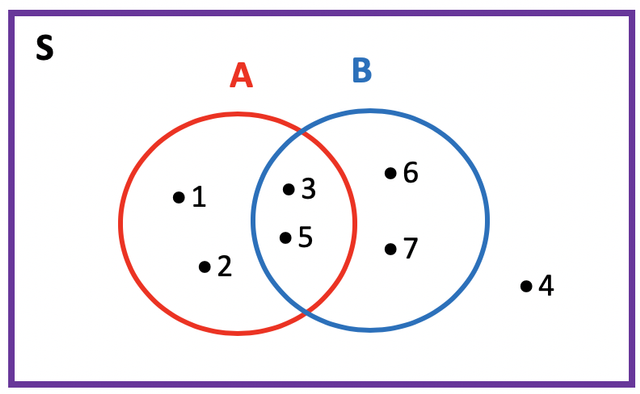
Rumus diagram venn akan menggambarkan dua himpunan yang saling berpotongan dan disebabkan karena memiliki kesamaan. Contohnya, jika ada himpunan A dan B, keduanya akan berpotongan apabila mempunyai kesamaan.
Oleh karena itu, hal ini berarti bahwa anggota yang masuk pada himpunan A masuk sebagai himpunan B. Nantinya himpunan A akan berpotongan dengan himpunan B dan bisa dituliskan dengan simbol A∩B.
5. Himpunan Ekuivalen
Dapat dikatakan bahwa himpunan A maupun himpunan B ekuivalen jika anggota dari kedua himpunan memiliki jumlah yang sama. Untuk himpunan A ekuivalen dan himpunan B bisa dituliskan n(A)=n(B).
Pada diagram venn memiliki empat hubungan antara himpunan seperti gabungan irisan komplemen himpunan maupun selisih himpunan. Supaya lebih paham mengenai himpunan ekuivalen, silahkan Anda melihat hubungan berikut ini:
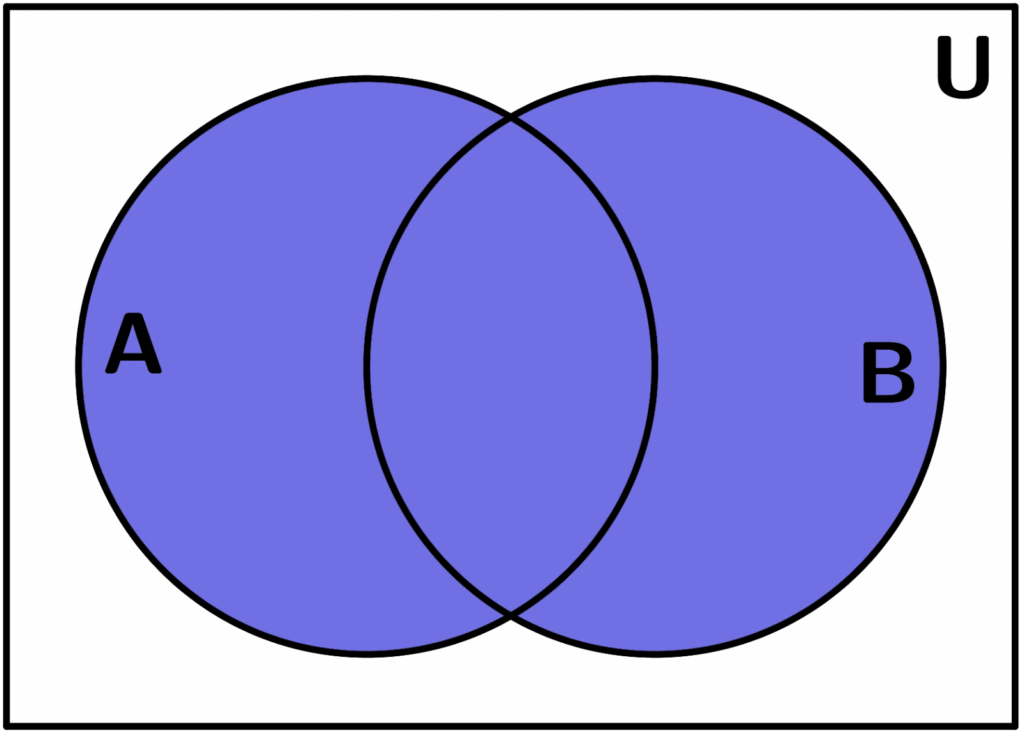
Gabungan
Gabungan adalah himpunan A dan B yang merupakan jumlah himpunan. Anggotanya adalah himpunan A maupun anggota himpunan B. Bisa juga anggota keduanya untuk gabungan himpunan A maupun B ini akan dinotasikan menggunakan rumus A ∪ B = {x | x ∈ A atau x ∈ B}.
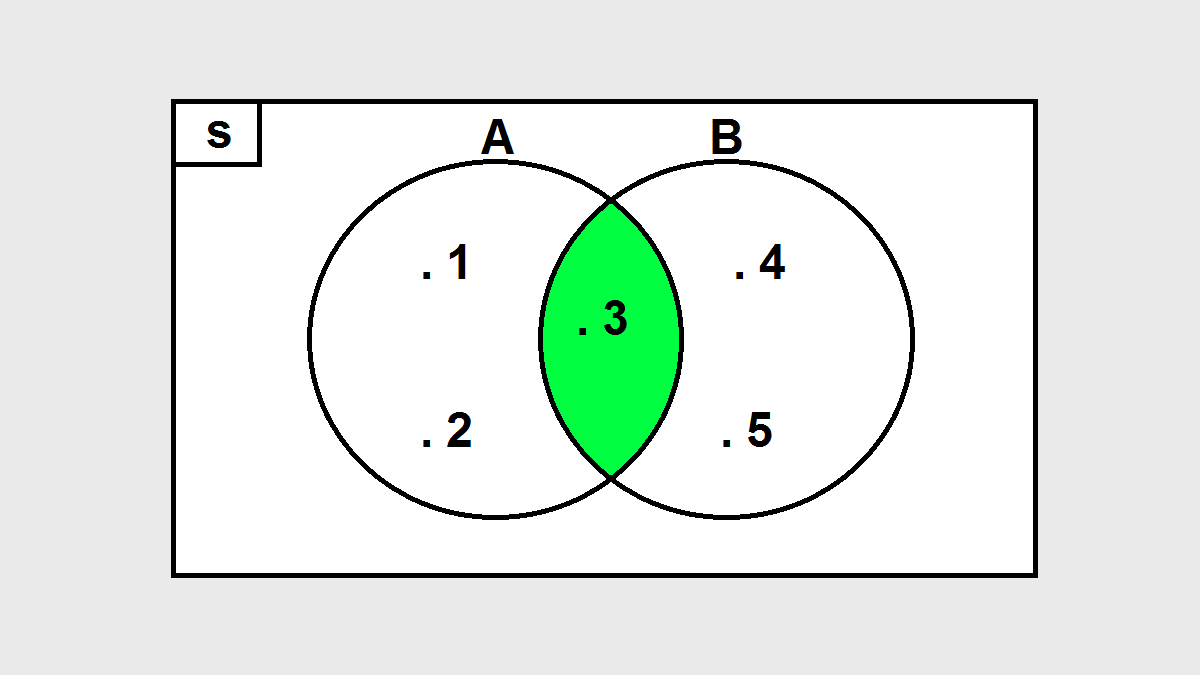
Irisan
Hubungan irisan pada himpunan A dan B merupakan himpunan yang mana para anggotanya berada di dalam himpunan A maupun himpunan B. Anda harus memperhatikan bahwa di antara kedua himpunan tersebut memiliki dua anggota yang sama.
Dari kesamaan inilah yang dapat dikatakan bahwa irisan dari himpunan A maupun B akan dituliskan sebagai A∩B) = {3,4,5}.
Komplemen
Komplemen yang ada di himpunan A merupakan himpunan yang memiliki anggotanya adalah himpunan semesta.
Akan tetapi bukan dari anggota himpunan A, untuk semua anggota bukan dari anggota A dan akan membentuk himpunan baru yaitu {0,2,4,6,8}. Komplemen dari himpunan A ini adalah = {0,2,4,6,8}
Aturan Membuat Diagram Venn
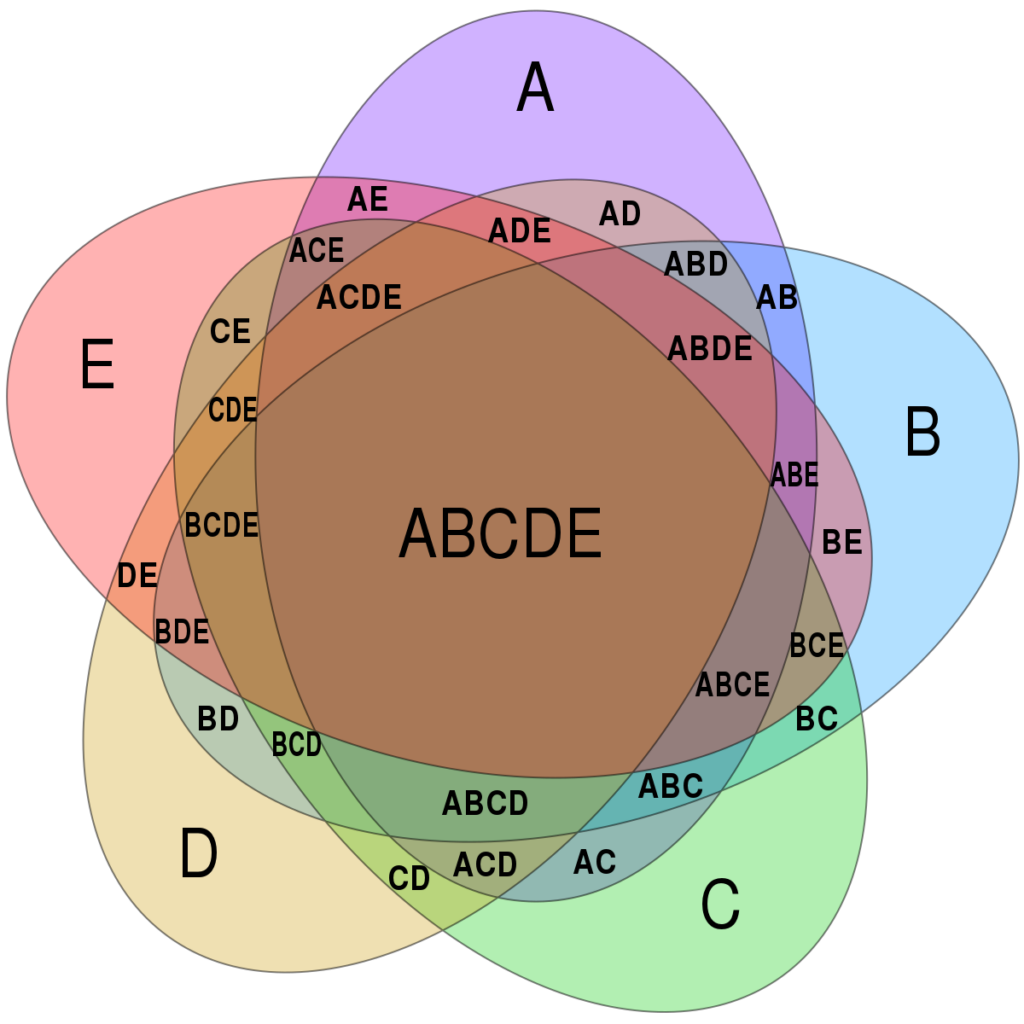
Dalam pembuatan rumus diagram venn 4 himpunan tentunya tidaklah dilakukan secara asal-asalan, karena harus memenuhi syarat maupun ketentuan yang diberlakukan.
Untuk meminimalisir terjadinya kesalahan, berikut ini aturan pembuatan diagram venn yang harus diperhatikan, yaitu:
- Himpunan semesta yang digunakan pada diagram harus berbentuk persegi panjang dan semua data yang digunakan berfokus pada diagram.
- Himpunan lain juga menjadi fokus pembuatan diagram dan dikelompokkan dalam satu lingkaran maupun kurva tertutup.
- Anggota pada setiap himpunan akan dinyatakan titik per datanya.
- Apabila terdapat anggota himpunan yang memiliki nilai tidak terhingga, otomatis setiap anggota tidak harus menggunakan titik pada setiap datanya.
Pembuatan diagram venn memang tidak terlalu sulit dilakukan apabila Anda mengetahui bagaimana teknik dan syarat pembuatannya. Dengan informasi rumus diagram venn yang ada di atas, diharapkan supaya Anda bisa memahami diagram venn secara mendalam.