Pengertian Bilangan Biner
Bilangan biner adalah sebuah sistem penulisan angka digital yang hanya menggunakan dua simbol yaitu bilangan 0 dan 1. Sistem bilangan biner merupakan salah satu dari empat sistem bilangan yang diterapkan pada komputer, dimana nilai dari 1 byte bilangan biner adalah 8 bit. Bilangan biner juga disebut sebagai bilangan yang menggunakan 2 radiks / baris (0 dan 1).
Cara penulisan bilangan biner biasanya terdiri dari delapan digit angka. Dalam penerapan rangkaian digital biasanya bilangan biner 1 mempunyai arti nyala dan bilangan 0 adalah mati. Sementara dalam sebuah sistem komputer, kode biner diartikan sebagai ukuran dari komputasi sebuah data. Contohnya:
1 Byte (B) = 8 bits = 8 digit biner
1 Kilo Byte (KB) = 1.000 Bytes = 8.000 bits
1 Mega Byte (MB) = 1.000.000 Bytes = 1.000 KB = 8.000.000 bits
1 Giga Byte (GB) = 1.000.000.000 Bytes = 1.000 MB = 8.000.000.000 bits
1 Tera Byte (TB) = 1 Triliun Bytes = 1.000 GB = 1 Triliun bits
Cara Konversi Bilangan Biner
Cara konversi bilangan dilakukan saat ingin merubah bentuk dari bilangan satu ke bilangan lainnya. Sebenarnya proses konversi akan menjadi mudah jika Anda mengetahui bagaimana caranya, untuk itu mari simak sub bab artikel ini untuk mengetahui semua hal tentang konversi bilangan biner. Ada empat kunci penting yang perlu Anda ketahui yaitu:
- Bilangan biner adalah bilangan yang hanya mempunyai dua basis yaitu 0 dan 1.
- Bilangan Oktal adalah bilangan yang mempunyai delapan basis yaitu dari 0 hingga 7.
- Bilangan desimal adalah bilangan yang mempunyai sepuluh basis yaitu dari 0 hingga
- Bilangan heksadesimal adalah bilangan yang mempunyai enam belas basus yaitu dari 0 hingga F.
Berikut ini adalah tabel untuk memperjelas nilai-nilai dari sistem bilangan.
| Biner | Desimal | Oktal | Heksadesimal |
| 0000 | 0 | 0 | 0 |
| 0001 | 1 | 1 | 1 |
| 0010 | 2 | 2 | 2 |
| 0011 | 3 | 3 | 3 |
| 0100 | 4 | 4 | 4 |
| 0101 | 5 | 5 | 5 |
| 0110 | 6 | 6 | 6 |
| 0111 | 7 | 7 | 7 |
| 1000 | 8 | 10 | 8 |
| 1001 | 9 | 11 | 9 |
| 1010 | 10 | 12 | A |
| 1011 | 11 | 13 | B |
| 1100 | 12 | 14 | C |
| 1101 | 13 | 15 | D |
| 1110 | 14 | 16 | E |
| 1111 | 15 | 17 | F |
A. Penulisan Sistem Bilangan
Untuk cara menulis sistem bilangan adalah dengan menambahkan tanda kurung di akhir bilangannya, berikut adalah contoh penulisan dari sistem bilangan.
Bilangan Biner 1111 1010 (2)
Bilangan Oktal 12 (8)
Bilangan Heksadesimal F4 (16)
Bilangan Desimal 111 (10)
B. Konversi Bilangan Biner ke Desimal
Pada dasarnya untuk mengkonversi bilangan biner ke desimal adalah dengan menggunakan prinsip 2 pangkat x atau 2x dan cara membacanya diawali dari kanan ke kiri, untuk lebih mempermudah pemahaman silahkan simak tabel berikut ini:
| Digit | Ke-7 | Ke-6 | Ke-5 | Ke-4 | Ke-3 | Ke-2 | Ke-1 | Ke-0 |
| Biner | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Pangkat | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| Desimal | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Seperti yang diperlihatkan pada tabel di atas, bahwa nilai digit pertama bilangan biner adalah 1, digit kedua adalah 2, dan seterusnya. Untuk lebih jelasnya perhatikan contoh berikut ini.
1. Berapa nilai desimal dari bilangan biner 1101 0001(2) dan 111(2)?
Untuk cara termudahnya adalah dengan menjumlahkan semua nilai desimal dari bilangan biner yang berdigit 1, lalu bagaimana jika bilangan biner tidak 8 digit? Maka semua bilangan sebelumnya bernilai 0.
| Digit | Ke-7 | Ke-6 | Ke-5 | Ke-4 | Ke-3 | Ke-2 | Ke-1 | Ke-0 | Hasil |
| Desimal | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 1101 0001(2) | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 128+64+16+1 = 209 |
| 111(2) | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 4+2+1=7 |
Jadi nilai dari 1101 0001(2) = 209(10) dan 111(2) = 7(10)
C. Konversi Bilangan Desimal ke Biner
Untuk melakukan konversi bilangan dari desimal ke biner caranya sama-sama menggunakan tabel diatas, hanya saja Anda harus menghitung di digit berapa yang akan digunakan supaya hasilnya sama dengan nilai desimal yang dicari. Contoh Ada angka desimal 11 maka nilai binernya dapat diperoleh dari penjumlahan desimal (8+2+1), digit yang digunakan diberi angka 1 dan digit yang tidak digunakan diberi angka 0. Berikut detailnya.
| Digit | Ke-7 | Ke-6 | Ke-5 | Ke-4 | Ke-3 | Ke-2 | Ke-1 | Ke-0 | Hasil |
| Desimal | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
| 11(10) | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0000 1011(2) |
Jadi nilai dari 11(10) = 0000 1011(2)
D. Konversi Bilangan Biner ke Oktal
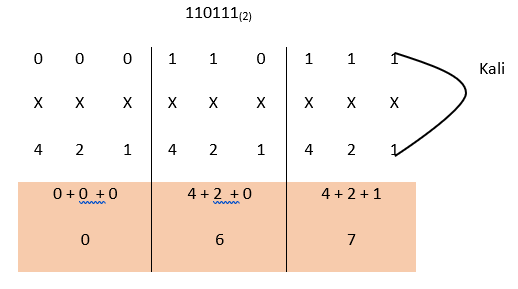
Untuk melakukan konversi bilangan biner ke oktal, Anda hanya perlu mengelompokan bilangan menjadi tiga digit, lalu nilainya diubah dalam bentuk desimal. Contohnya berapakah nilai oktal dari bilangan biner 110111(2)?
Jadi nilai oktal dari bilangan biner 110111(2) = 067(8).
E. Konversi Bilangan Oktal ke Biner
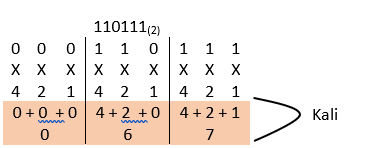
Konversi bilangan dari oktal ke biner sama halnya dengan konversi dari biner ke oktal, yaitu dengan membagi bilangan menjadi tiga bagian (satu bagian tiga digit). Contohnya berapa bilangan biner dari 137(8)?
Jadi nilai biner dari bilangan 137(8) = 001 011 111(2)
F. Konversi Bilangan Biner ke Heksadesimal
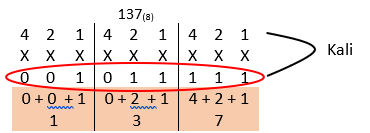
Konversi bilangan biner ke heksadesimal caranya mudah cukup membagi bilangan menjadi dua bagian, tiap bagiannya terdiri dari empat digit. Contoh 1010 1111 (2) berapakah nilai bilangan heksadesimalnya?
Jadi nilai heksadesimal dari 1010 1111(2) = AF(16)
G. Konversi Bilangan Heksadesimal ke Biner
Konversi dari heksadesimal ke biner sama dengan konversi dari biner ke heksadesimal yaitu dengan membagi menjadi dua bagian dimana tiap bagian ada empat digit. Contoh berapa nilai biner dari bilangan 7B(16)? Sebelumnya B=11
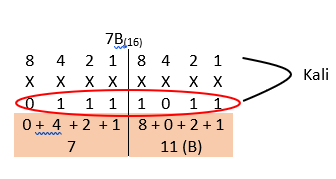
Jadi nilai dari 7B(16) = 0111 1011(2)