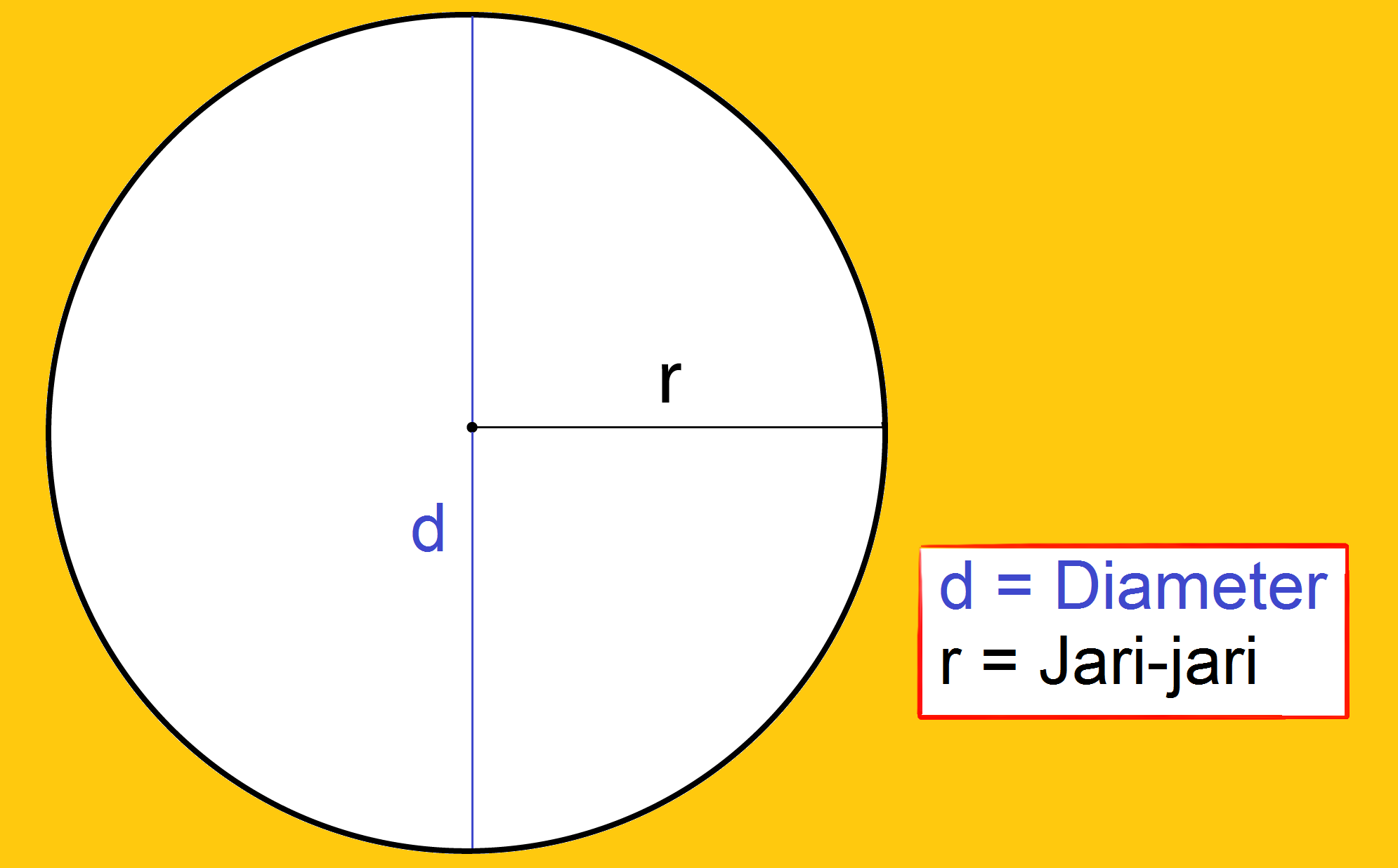
Lingkaran adalah bangun datar dua dimensi yang hanya memiliki luas dan keliling saja. Ada banyak contoh benda dalam kehidupan sehari-hari yang memiliki bentuk lingkaran. Bangun dua dimensi ini tersusun oleh bagian-bagian lingkaran seperti jari-jari, diameter, apotema, juring, dan sebagainya.
Contoh bangun yang memiliki bentuk lingkaran adalah koin logam, ban kendaraan, jam dinding, piring, teflon, alas cangkir dan lainnya. Karena diaplikasikan dalam berbagai bidang kehidupan, maka materi mengenai lingkaran harus dipahami untuk menghitung luas dan keliling bangun tersebut.
Pengertian Lingkaran
Lingkaran adalah bangun dua dimensi berupa kurva tertutup yang dibentuk oleh kumpulan titik dengan jarak yang diukur dari titik pusat adalah sama. Kumpulan titik yang ada di sekitar titik pusat lingkaran mempunyai jarak yang sama.
Jarak dari titik pusat ke titik pada lingkaran disebut sebagai jari-jari dan nilainya adalah tetap diukur dari titik keliling lingkaran manapun. Jari-jari merupakan salah satu unsur atau bagian lingkaran yang penting untuk mengukur luas dan keliling.
Lingkaran tidak memiliki volume karena merupakan objek geometri berbentuk dua dimensi. Bangun datar ini banyak diaplikasikan di berbagai bidang kehidupan seperti desain arsitektur bangunan, ban kendaraan, koin dan lainnya.
Daftar Bagian-Bagian Lingkaran
Lingkaran tersusun dari beberapa unsur yang harus diketahui untuk menghitung luas dan keliling bangun lingkaran. Unsur atau bagian yang menyusun lingkaran cukup banyak mulai dari titik pusat, jari-jari, diameter dan lainnya. Berikut bagian-bagian lingkaran dan penjelasannya yang wajib dipahami:
1. Titik Pusat Lingkaran
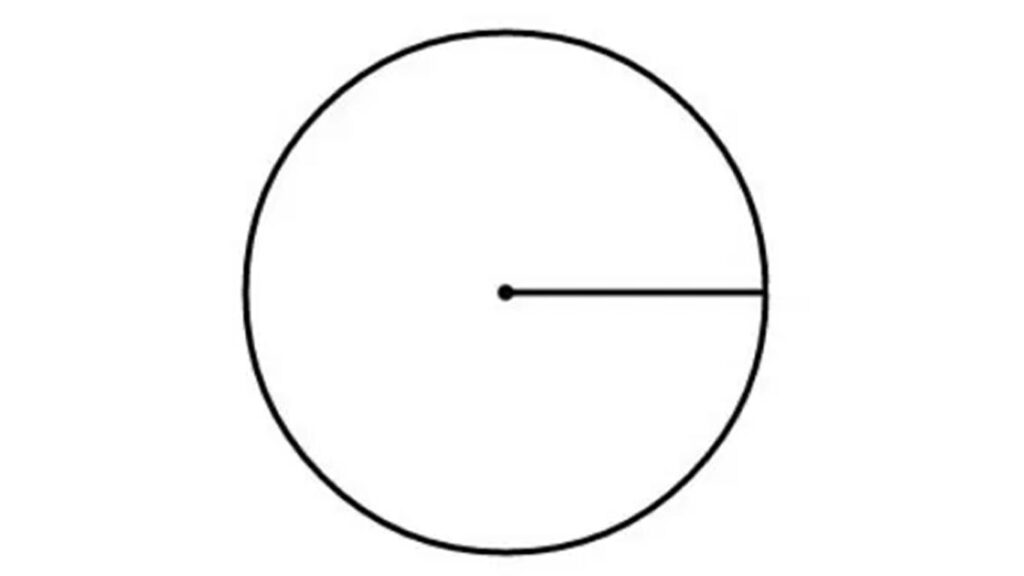
Titik pusat lingkaran merupakan titik yang berada tepat di tengah-tengah lingkaran sehingga jarak titik pusat dari titik di kurva melengkung sekeliling lingkaran adalah sama. Titik pusat lingkaran biasanya akan dituliskan menggunakan lambang O.
2. Jari-Jari (r)
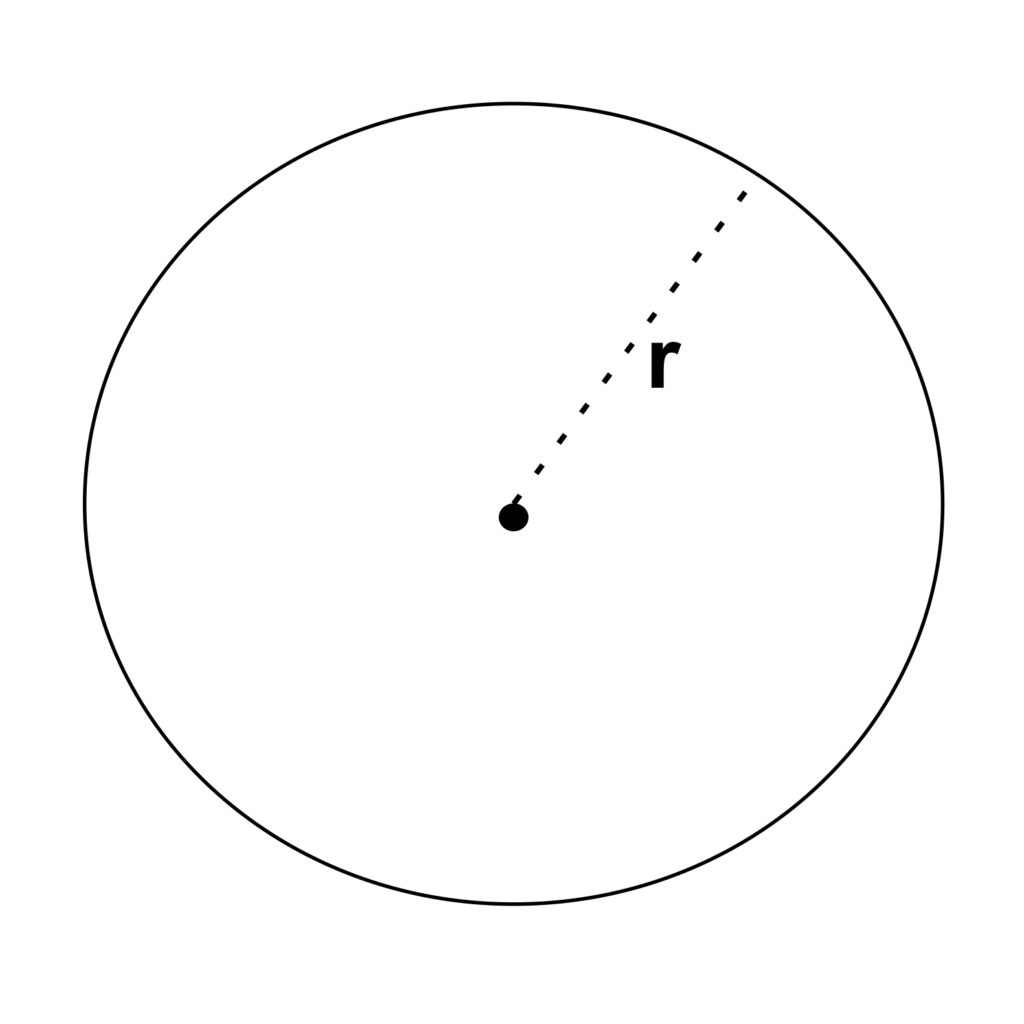
Jari-jari lingkaran merupakan jarak yang dihitung dari titik terluar lingkaran pada kurva melengkung menuju titik pusat lingkaran. Ukuran panjang jari-jari lingkaran adalah tetap meskipun diukur dari titik kurva melengkung yang berbeda.
Jari-jari lingkaran biasanya dilambangkan menggunakan huruf r dengan nilai setengah dari panjang diameter lingkaran.
r = ½ d
3. Diameter Lingkaran (d)
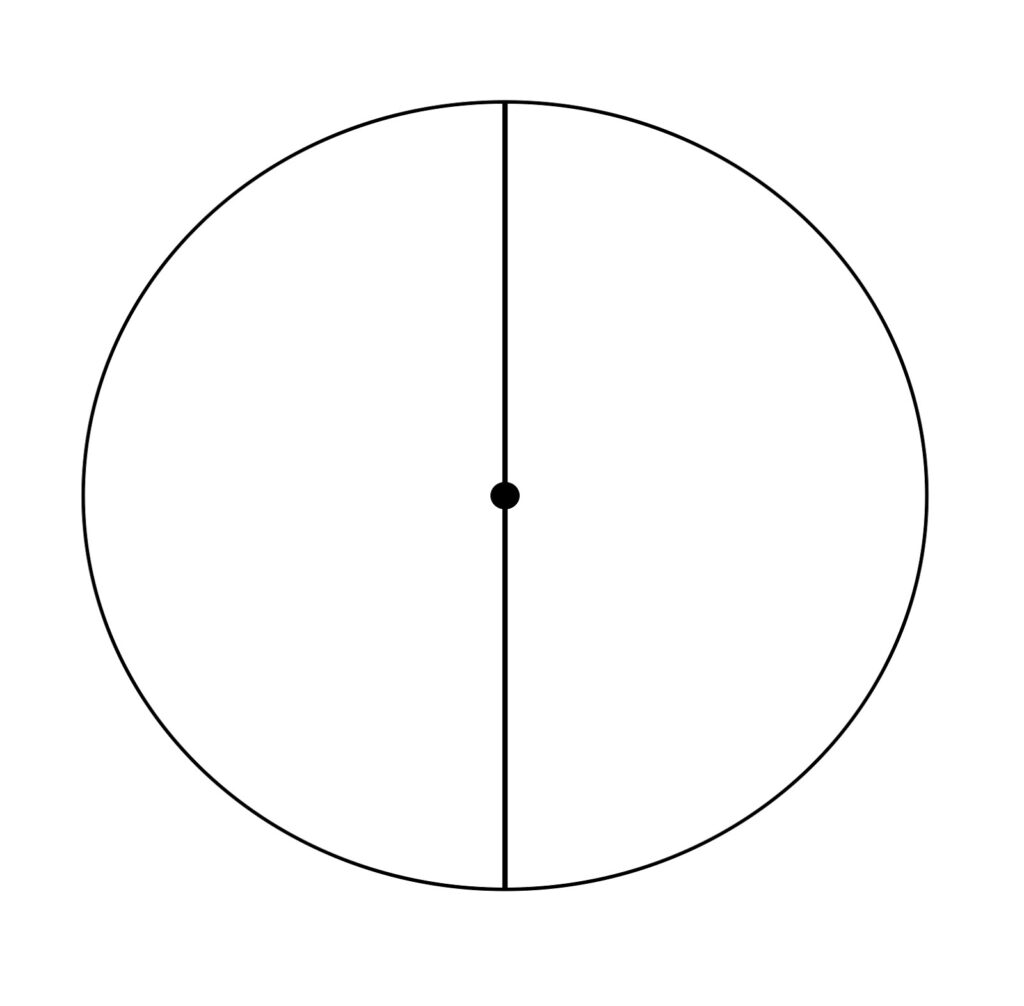
Diameter lingkaran adalah jarak yang dihitung dari titik paling luar lingkaran pada kurva melengkung ditarik lurus melalui titik pusat lingkaran ke titik terluar lingkaran pada kurva melengkung di seberangnya.
Karena melewati titik pusat lingkaran dari kedua ujung titik kurva melengkung maka panjang dari diameter lingkaran adalah dua kali panjang jari-jarinya. Diameter lingkaran dilambangkan dengan huruf d.
d = 2 r
4. Juring Lingkaran
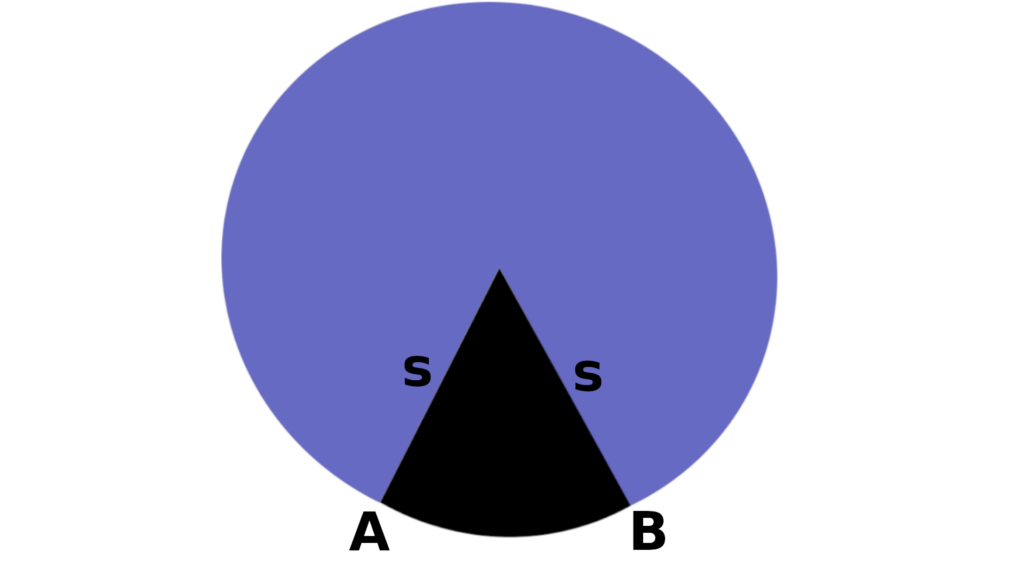
Juring adalah bagian dari lingkaran berupa area di dalam kurva melengkung atau busur yang dibatasi oleh dua buah jari-jari. Juring lingkaran dibedakan ke dalam dua macam yakni juring lingkaran besar dan juring kecil.
Kedua juring ini dibedakan berdasarkan panjang busur yang membatasinya. Juring lingkaran besar diapit oleh busur yang besar sementara juring lingkaran kecil diapit oleh busur yang berukuran lebih kecil.
5. Tali Busur
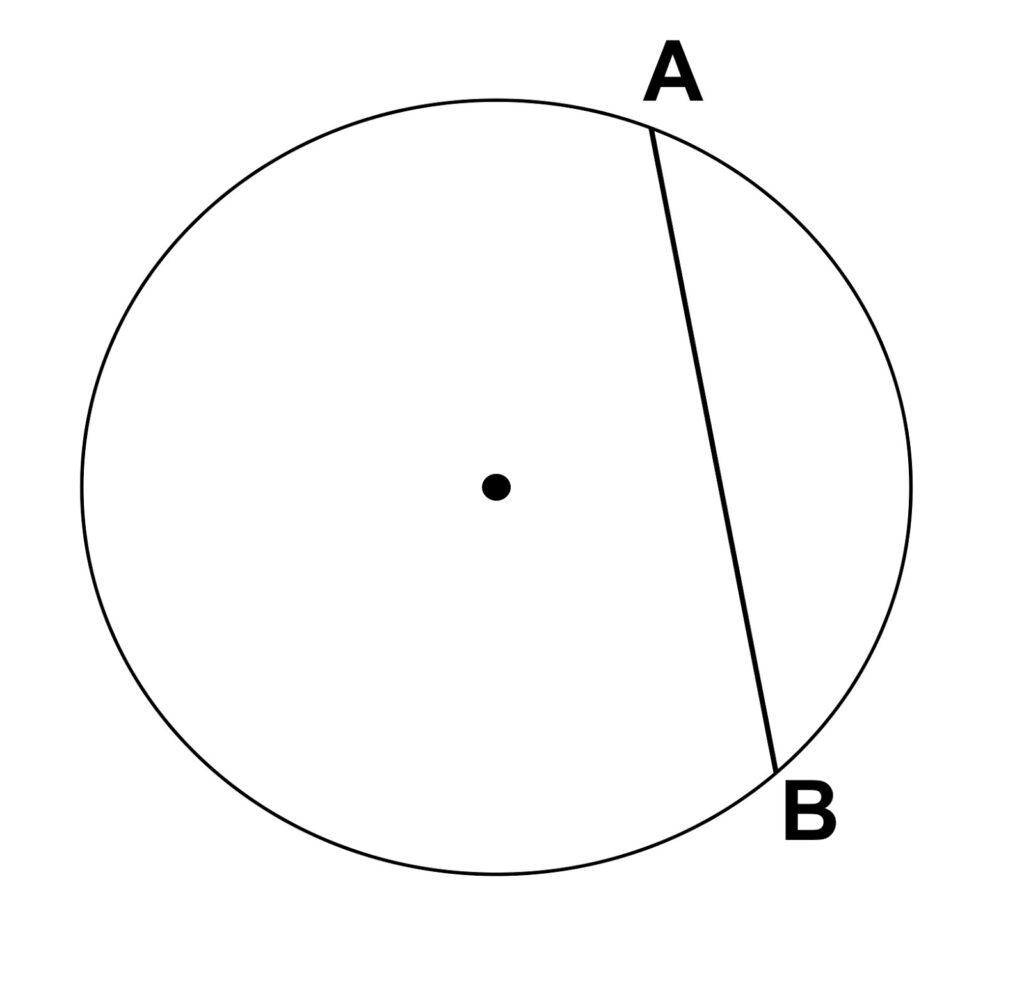
Tali busur merupakan unsur lingkaran yang terbuat dari garis lurus yang ditarik sehingga menghubungkan kedua titik pada kurva melengkung lingkaran namun tidak melalui titik pusat.
Tali busur berbeda dari diameter lingkaran karena tidak melalui titik pusat. Tali busur ini nantinya akan membentuk tembereng pada lingkaran.
6. Busur
Busur merupakan unsur lingkaran berbentuk garis lengkung atau kurva melengkung yang membentuk lingkaran. Busur lingkaran dibedakan menjadi dua macam yaitu busur kecil dan busur besar.
Busur besar adalah busur lingkaran dengan panjang lebih dari setengah ukuran keliling lingkaran. Sementara busur kecil memiliki ukuran di bawah setengah keliling lingkaran.
7. Tembereng
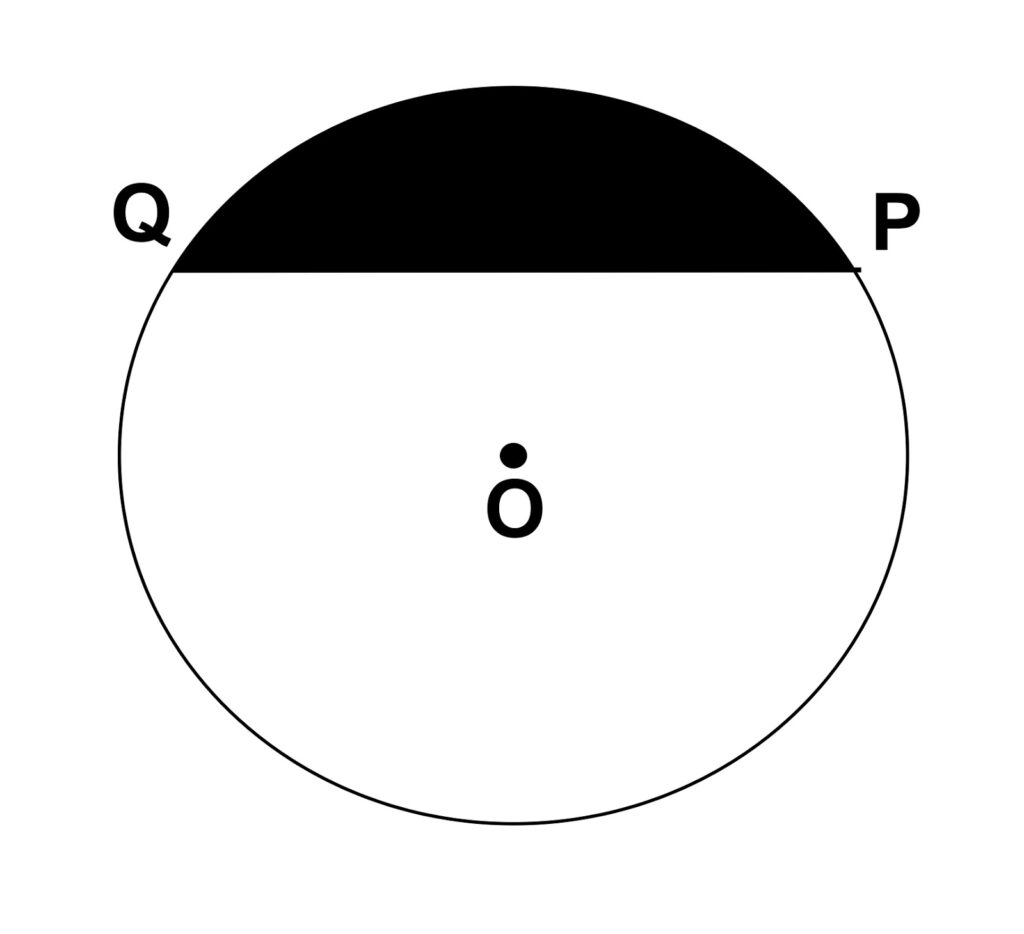
Tembereng lingkaran adalah salah satu dari bagian lingkaran yang diapit oleh sebuah busur lingkaran dan tali busur. Sebagaimana juring lingkaran, tembereng juga terdiri dari dua jenis berdasarkan busur lingkarannya yaitu tembereng kecil dan tembereng besar.
Tembereng kecil merupakan area pada lingkaran yang dibatasi busur kecil lingkaran dan sebuah tali busur. Sementara tembereng besar adalah daerah pada lingkaran yang dibatasi busur besar dan tali busur.
8. Apotema
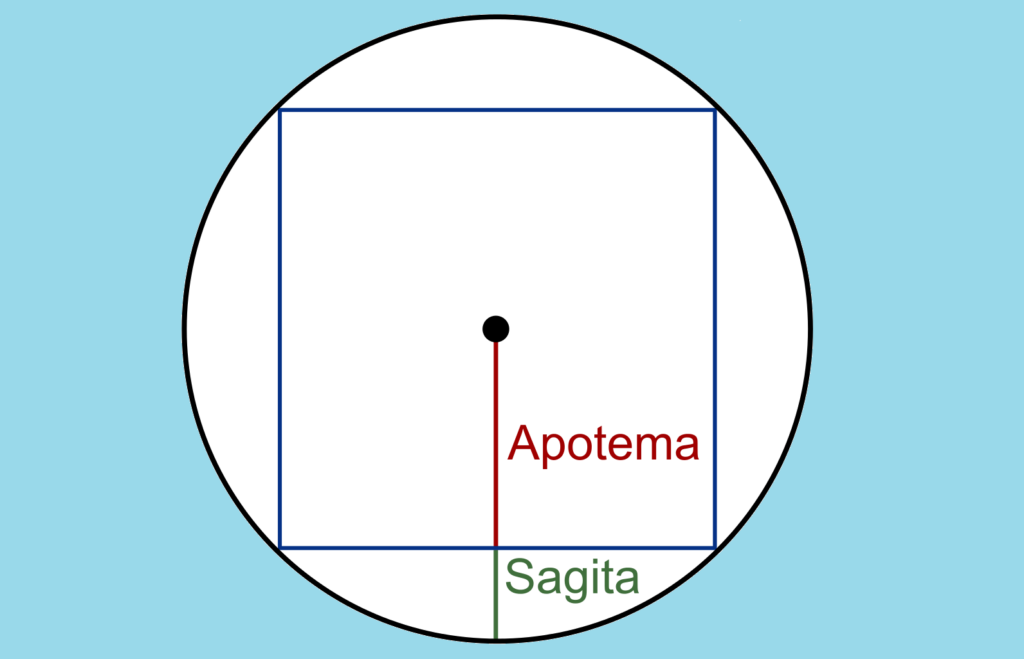
Apotema lingkaran adalah merupakan bagian dari lingkaran berupa garis tegak lurus yang diukur dari tali busur menuju titik pusat lingkaran. Karena merupakan garis tegak lurus maka ukuran apotema adalah yang terpendek.
9. Sudut Pusat
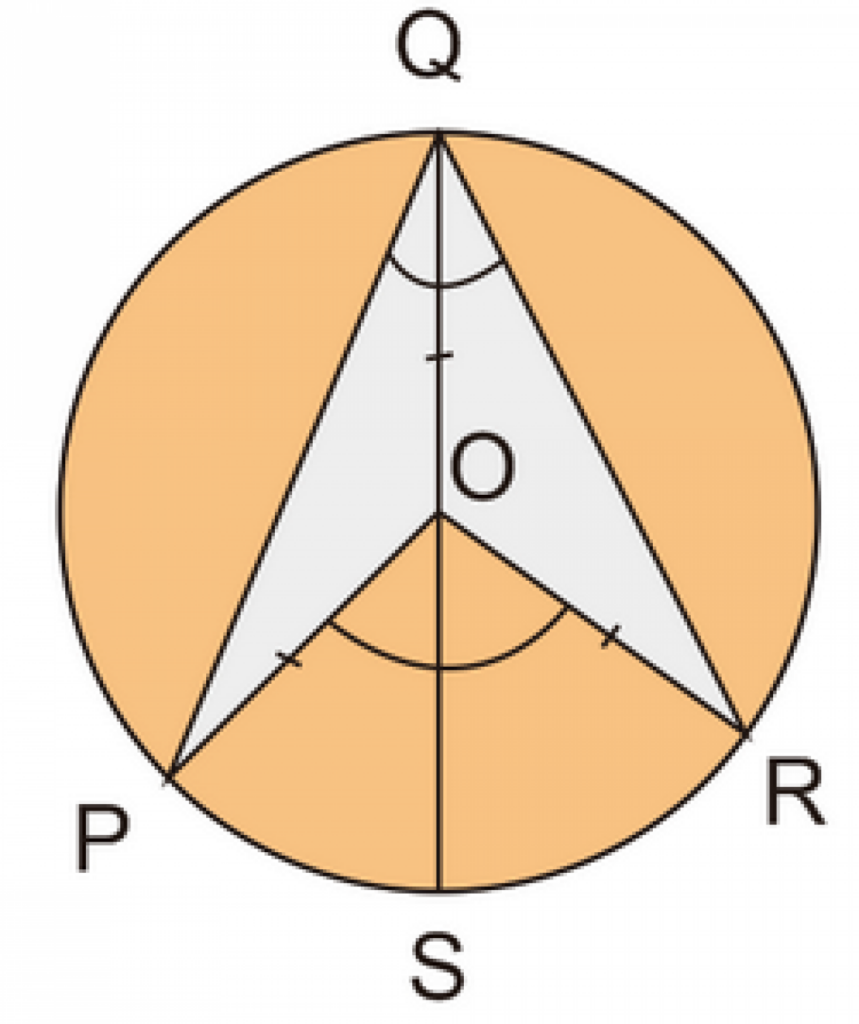
Sudut pusat merupakan sudut lingkaran yang terbentuk dari dua buah tali busur yang bertemu dengan satu titik di busur lingkaran.
Untuk memudahkan Anda memahami bagian-bagian lingkaran di bawah ini adalah gambar yang menunjukkan beberapa unsur atau bagian dari bangun geometri lingkaran meliputi jari-jari, diameter, tembereng, juring, busur, dan tali busur.
Kumpulan Rumus Lingkaran
Seperti yang diketahui bahwa lingkaran adalah bangun datar dua dimensi yang ditemukan dalam kehidupan sehari-hari. Oleh karena itu penting untuk mengetahui hubungan dari setiap bagian-bagian lingkaran dan rumusnya meliputi keliling lingkaran, luas lingkaran, luas juring dan sebagainya.
1. Rumus Keliling Lingkaran
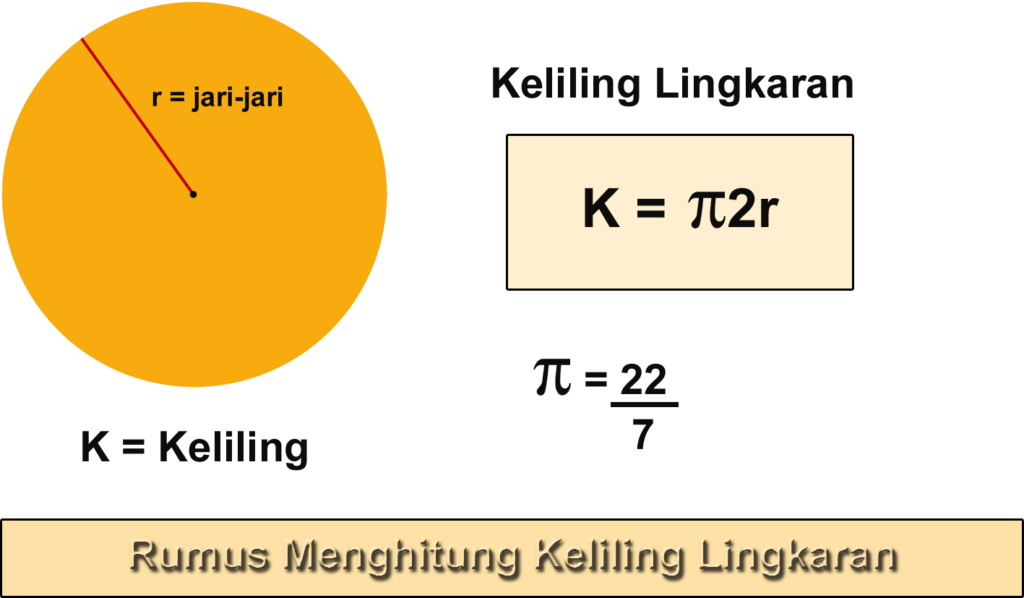
Keliling lingkaran merupakan ukuran panjang satu lintasan penuh yang dilalui sebuah benda berbentuk lingkaran yang berakhir di titik yang sama dengan titik awal mula.
Untuk menghitung keliling lingkaran membutuhkan informasi bagian-bagian lingkaran yakni ukuran jari-jari lingkaran atau bisa juga diameter lingkaran kemudian dikalikan dengan konstanta phi.
Jika diketahui jari-jari lingkaran bisa menggunakan rumus keliling lingkaran di bawah:
K = 2 x π x r
Jika diketahui diameter lingkaran bisa menggunakan rumus keliling lingkaran di bawah:
K = π x D
Keterangan:
r = jari-jari lingkaran (cm)
D = diameter lingkaran (cm)
K = Keliling lingkaran (cm)
π = konstanta phi, bernilai tetap yaitu 22/7 atau 3,14
2. Rumus Luas Lingkaran
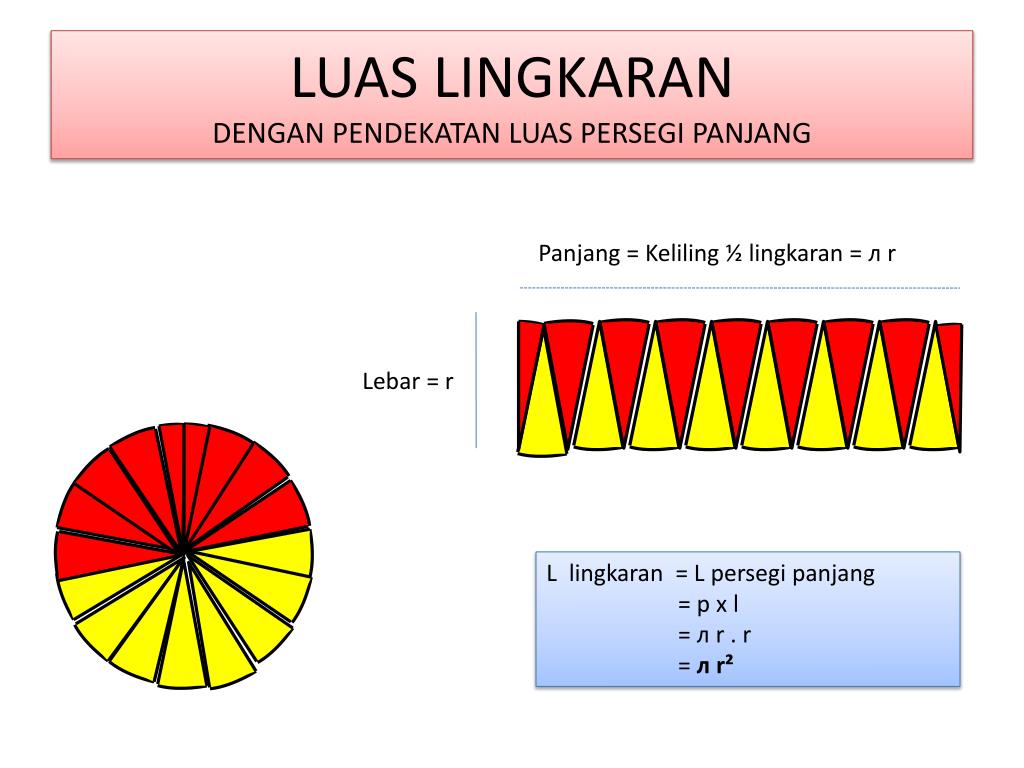
Sebagaimana rumus menghitung keliling lingkaran, untuk menghitung luas lingkaran juga bisa menggunakan informasi jari-jari maupun diameter lingkaran. Luas lingkaran didefinisikan sebagai area tertutup yang dikelilingi oleh kurva melengkung di sekelilingnya.
Untuk menghitung luas lingkaran dengan mengalikan konstanta phi dengan jari-jari lingkaran maupun diameter lingkaran.
Berikut adalah rumus menghitung luas lingkaran jika jari-jari lingkaran diketahui:
L = π. atau L = π. r. r
Keterangan:
r = jari – jari lingkaran (cm)
L = luas lingkaran (cm²)
Sementara jika informasi yang diketahui adalah diameter lingkaran (d), maka untuk menghitung luas lingkaran bisa menggunakan persamaan di bawah ini:
L = π.
L = π.
L = π. ¼ atau L = ¼ π.
Keterangan:
d = diameter lingkaran (cm)
Soal Lingkaran dan Penjelasan
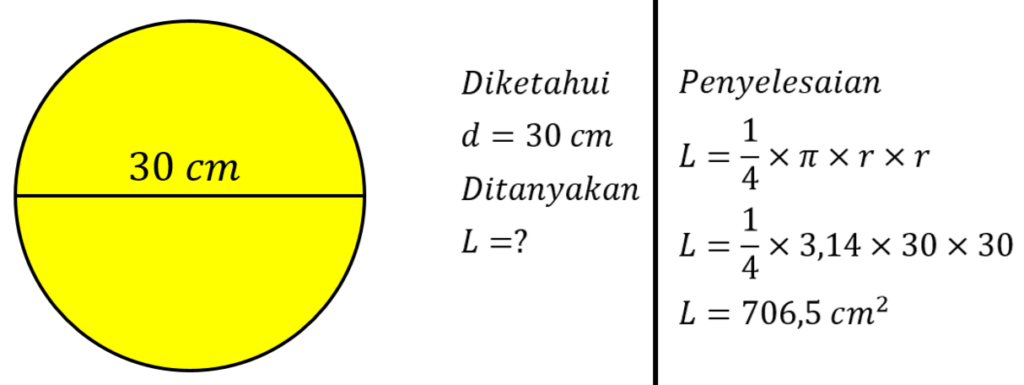
Hitunglah berapa keliling dan luas lingkaran dengan jari-jari 10 cm.
Jawab:
K = 3,14 x 20
K = 62,8 cm
L = 3,14 x r²
L = 3,14 x 100 = 314 cm²
Lingkaran adalah bangun datar dua dimensi yang terbentuk dari beberapa unsur atau bagian lingkaran. Bagian-bagian lingkaran terdiri dari titik pusat, jari-jari, diameter, juring, tembereng, apotema, busur, tali busur dan sebagainya.