5 Contoh Soal Rangkaian Campuran Beserta Pembahasan Singkat

Artikel kali ini akan menyajikan beberapa contoh soal mengenai rangkaian campuran dan juga pembahasannya, langsung saja menuju contoh soal pertama sebagai berikut:

1. Terdapat 3 buah resistor dimana R2 dan R3 di rangkai secara paralel kemudian terhubung seri dengan R1. Masing-masing nilai dari resistor adalah 160 KΩ, hitunglah nilai hambatan totalnya.

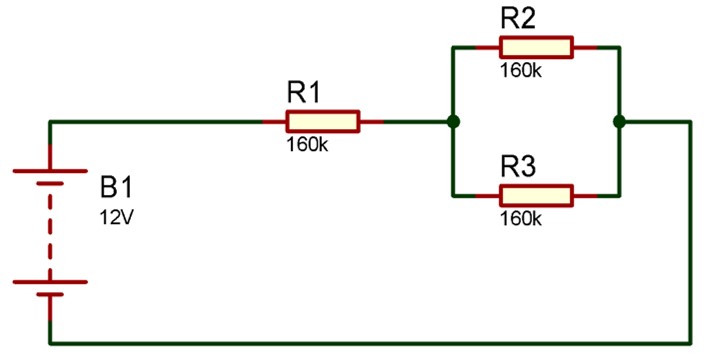
Pembahasan:

Diketahui:

• R1 = 160 KΩ
• R2 = 160 KΩ
• R3 = 160 KΩ
• V1 = 12 V

Ditanya R_total ?

Jawab:

#Untuk mengerjakan rangkaian campuran di atas, Anda perlu menyederhanakan rangkaian terlebih dahulu dengan cara menghitung hambatan total dari resistor yang dirangkai paralel.

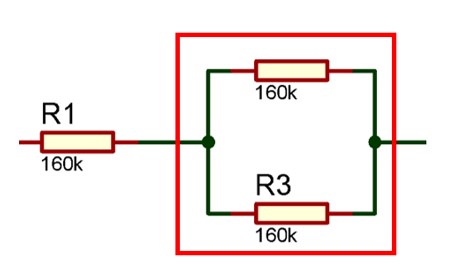
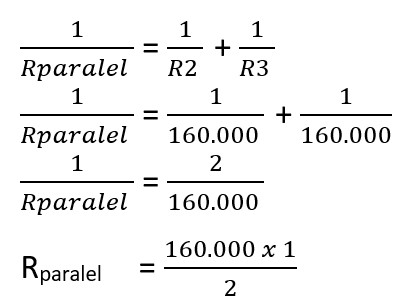
R_paralel       = 80.000 Ω = 80 KΩ

 

#Setelah rangkaian disederhanakan akan menjadi rangkaian seri seperti gambar dibawah, baru setelah itu Anda bisa menghitung nilai hambatan totalnya:

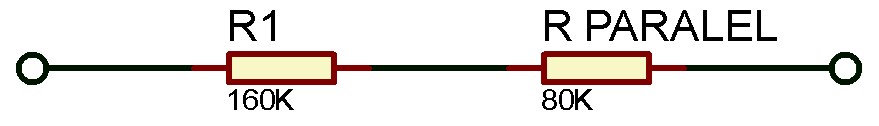
R_total  = R₁ + R_paralel

R_total  = 160 KΩ + 80 KΩ

R_total  = 240 KΩ = 240.000 Ω

Jadi nilai hambatan totalnya adalah 240.000 Ω.

 

2. Hitunglah nilai hambatan pengganti dari rangkaian resistor campuran berikut!

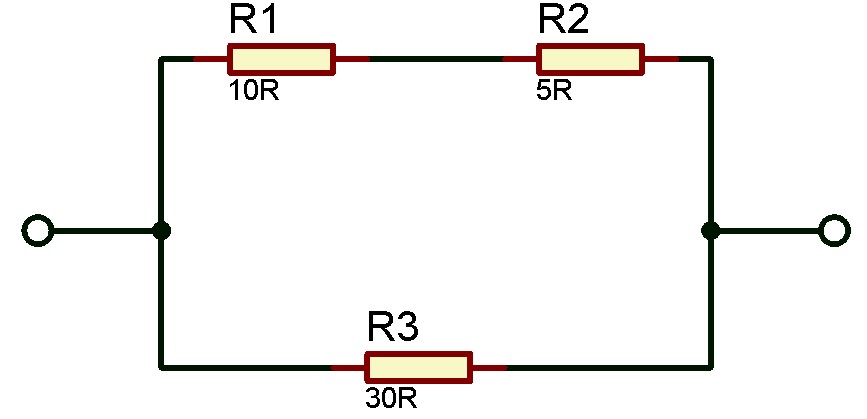
Pembahasan:

Diketahui

• R1 = 10 Ω
• R2 = 5 Ω
• R3 = 30 R

Ditanya R_pengganti?

Jawab:

#Saat menyelesaikan rangkaian campuran, pertama adalah dengan menyederhanakan rangkaian. Pada rangkaian diatas perlu disederhanakan dulu rangkaian serinya sebelum kita menghitung rangkaian paralel. Berikut perhitungan nilai hambatan pada rangkaian seri.

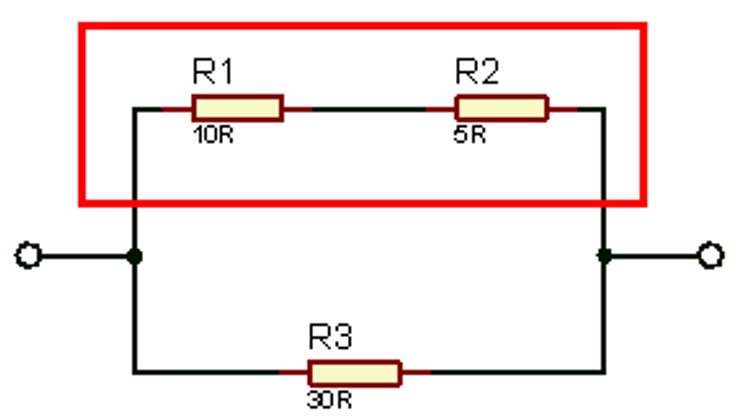
R_seri  = R₁ + R₂

R_seri  = 10 Ω + 5 Ω

R_seri  = 15 Ω

#Setelah menyederhanakan rangkaian, maka rangkaian campuran akan berbentuk menjadi rangkaian paralel. Anda dapat menghitung hambatan pengganti dengan rumus rangkaian paralel.

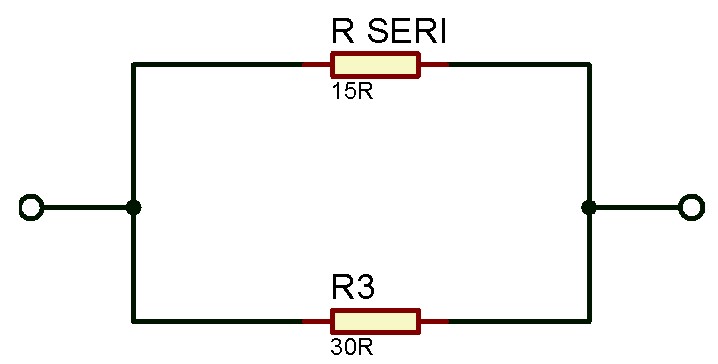
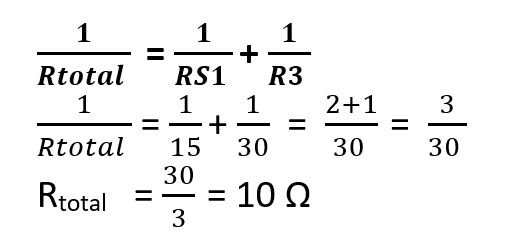
#Jadi, besar hambatan pengganti pada susunan itu adalah 10 Ω.

3. Tiga buah resistor tersusun secara paralel masing-masing nilainya adalah 2 Ω, 3 Ω, dan 6 Ω. Kemudian terhubung secara seri dengan hambatan bernilai 4,7 Ω. Berapakah nilai dari hambatan total pada rangkaian tersebut?

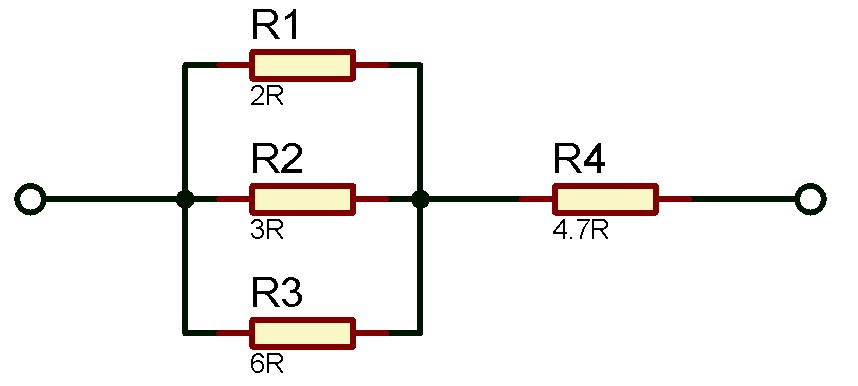
Pembahasan:

Diketahui

• R1 = 2 Ω
• R2 = 3 Ω
• R3 = 6 Ω
• R4 = 4.7 Ω

Ditanya R_total ?

Jawab:

#Untuk menyelesaikan rangkaian campuran diatas, caranya adalah dengan menyederhanakan rangkaian. Langkah pertama menghitung nilai pengganti dari rangkaian paralel, setelahnya baru menghitung rangkaian seri.

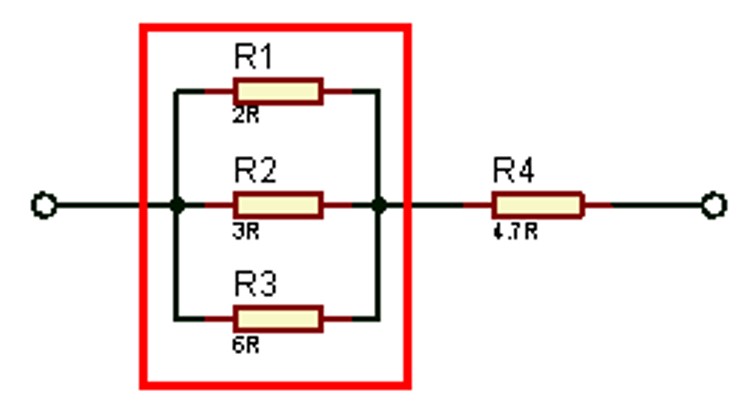
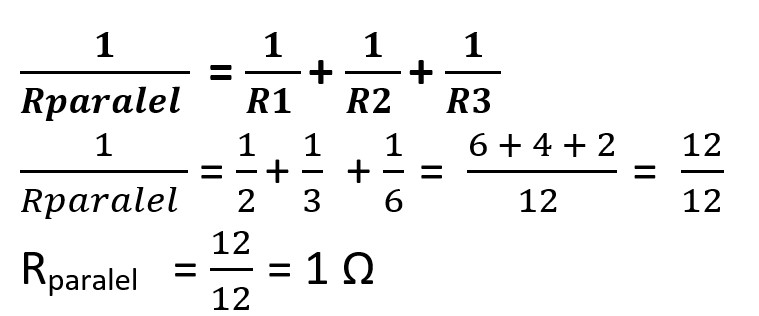
#Setelah disederhanakan rangkaian menjadi berbentuk seri seperti gambar rangkaian dibawah, lalu Anda dapat menghitung nilai hambatan total dengan rumus rangkaian seri.

R_seri  = R₁ + R₂

R_seri  = 1 Ω + 4,7 Ω

R_seri  = 5,7 Ω

#Jadi, besar hambatan total pada susunan itu adalah 5,7 Ω.

4. Hitunglah nilai hambatan pengganti dari gambar rangkaian resistor campuran berikut!

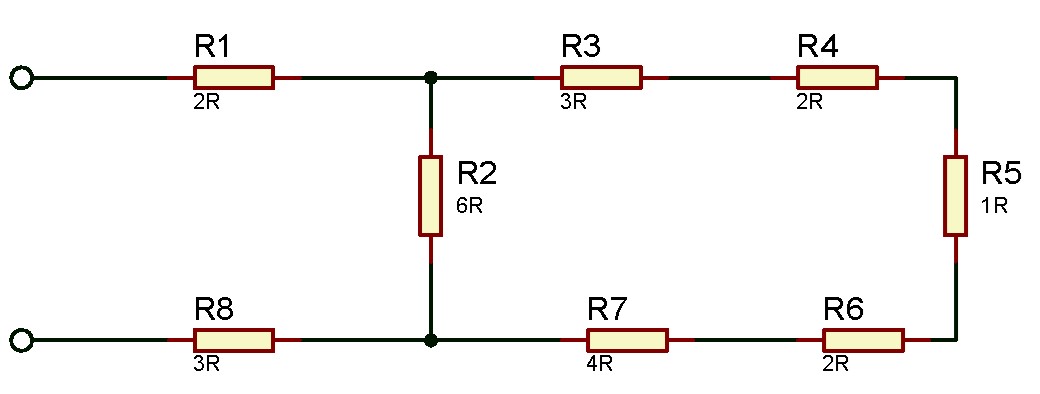
Pembahasan:

Diketahui

• R1 = 2 Ω
• R2 = 6 Ω
• R3 = 3 Ω
• R4 = 2 Ω
• R5 = 1 Ω
• R6 = 2 Ω
• R7 = 4 Ω
• R8 = 3 Ω

Ditanya R_pengganti ?

Jawab:

#Pada rangkaian campuran diatas komponen R3, R4, R5, R6, dan R7 terhubung secara seri. Maka Anda dapat menghitung nilai hambatan totalnya dari kelima resistor tersebut menggunakan rumus rangkaian seri.

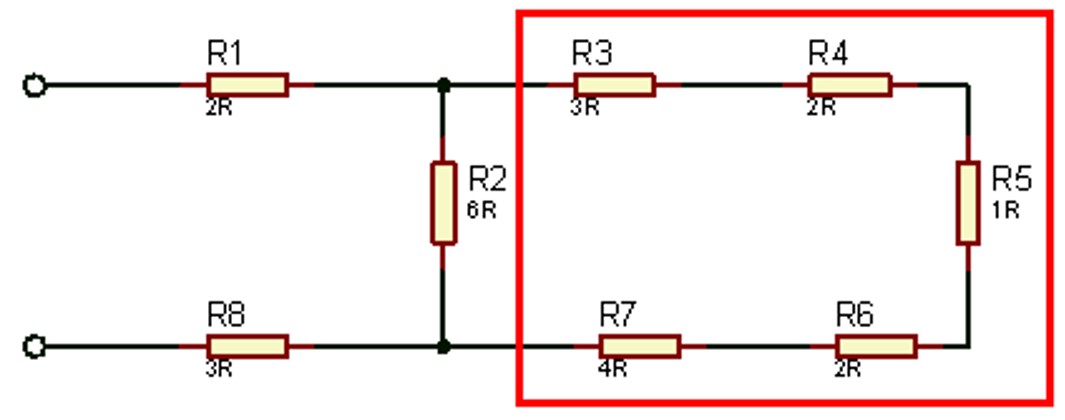
R_seri  = R₃ + R₄ + R₅ + R₆ + R₇

R_seri  =  3 + 2 + 1 + 2 + 4

R_seri  = 12 Ω

#Setelahnya maka rangkaian menjadi seperti berikut. karena R6 dan R seri terhubung secara paralel, maka berikutnya perhitungan menggunakan rumus paralel.

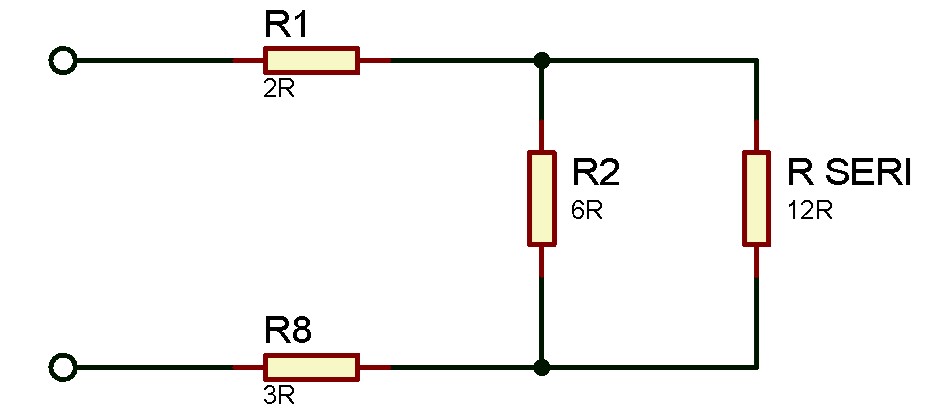
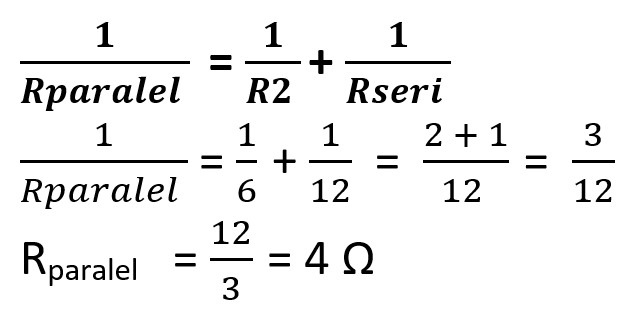
#Diperoleh penyederhanaan rangkaianya menjadi seperti gambar berikut, karena ketiga resistor menjadi terhubung secara seri. Maka kita hanya tinggal menjumlahkan saja nilai dari ketiga resistor tersebut.

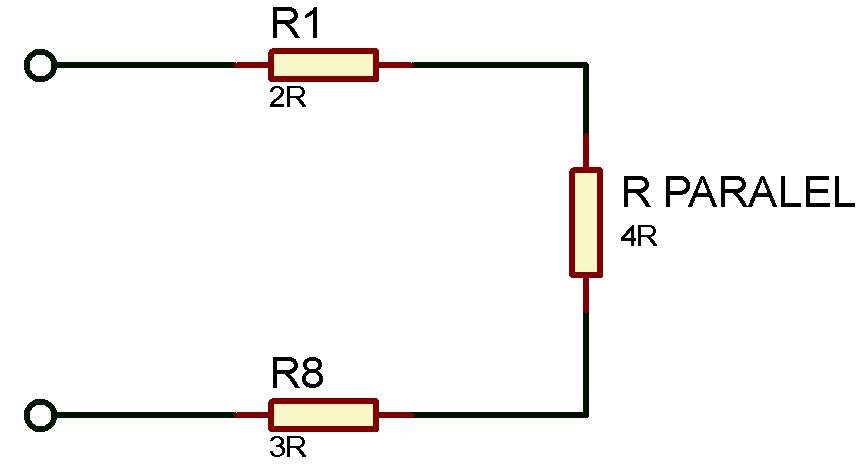
R_pengganti  = R₁ + R_paralel + R₈

R_pengganti  = 2 + 4 + 3

R_seri  = 9 Ω

#Jadi, hamabatan pengganti dari rangkaian campuran ini adalah 9 Ω.

5. Dua buah resistor masing-masing 10 Ω dan 2 Ω dirangkai secara seri kemudian dihubungkan secara paralel dengan dua buah resistor lainnya yang disusun seri. Kedua resistor tersebut masing-masing 8 Ω dan 4 Ω. Tentukanlah nilai hambatan total atau hambatan pengganti pada rangkaian tersebut?

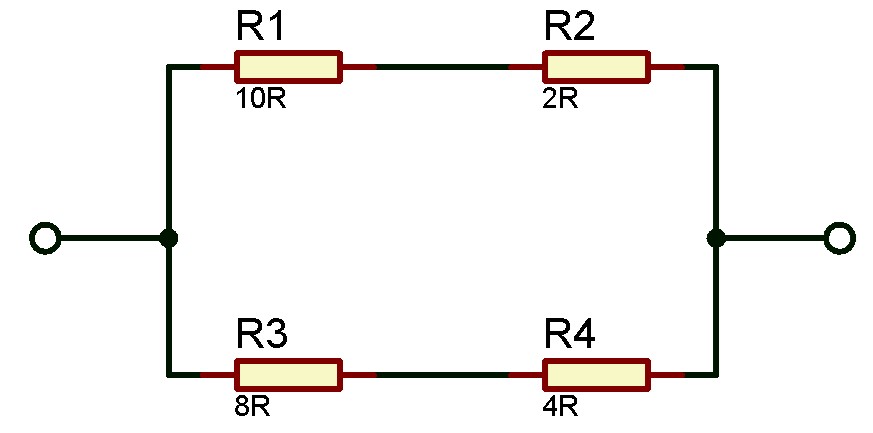
Pembahasan:

Diketahui

• R₁ =   10Ω
• R₂ =  2Ω
• R₃ =  8Ω
• R₄ =  4A

Ditanyakan: R_total ?

Jawab:

#Pada rangkaian campuran diatas kita perlu menyederhanakan rangkaian menjadi 3 tahapan, yang pertama adalah menghitung rangkaian seri pertama R1 dan R2, kemudian menghitung rangkaian seri kedua R3 dan R4, dan yang terakhir adalah menghitung hambatan total yang berbentuk paralel.

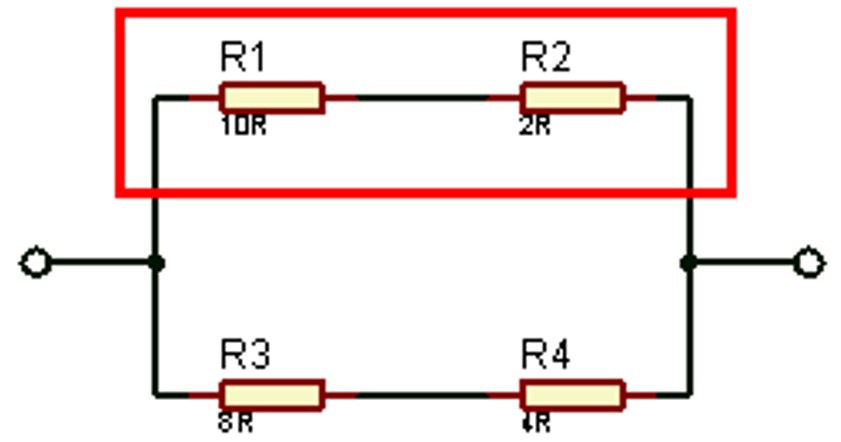
R_S1 = R₁ + R₂

R_S1 = 10 + 2

R_S1 = 12Ω

#Menghitung rangkaian seri kedua

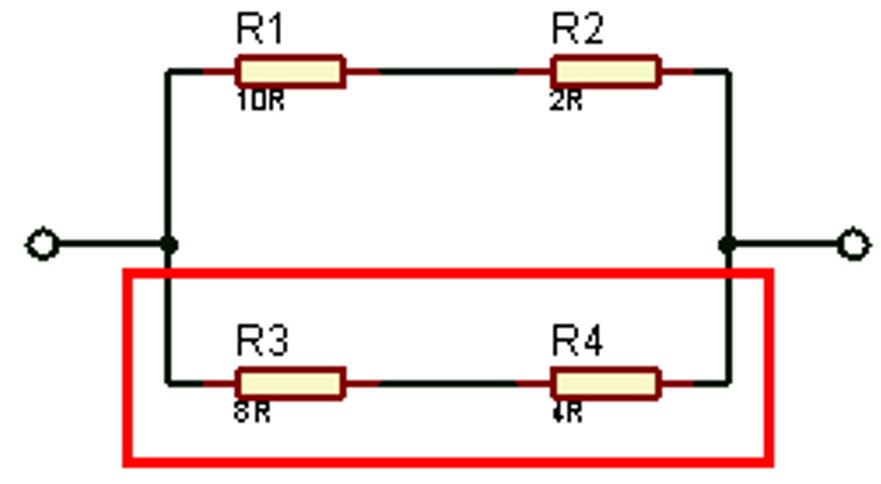
R_S2 = R₃ + R₄

R_S2 = 8 + 4

R_S2 = 12Ω

#Menghitung hambatan total dari rangkaian yang sudah disederhanakan, seperti gambar dibawah.

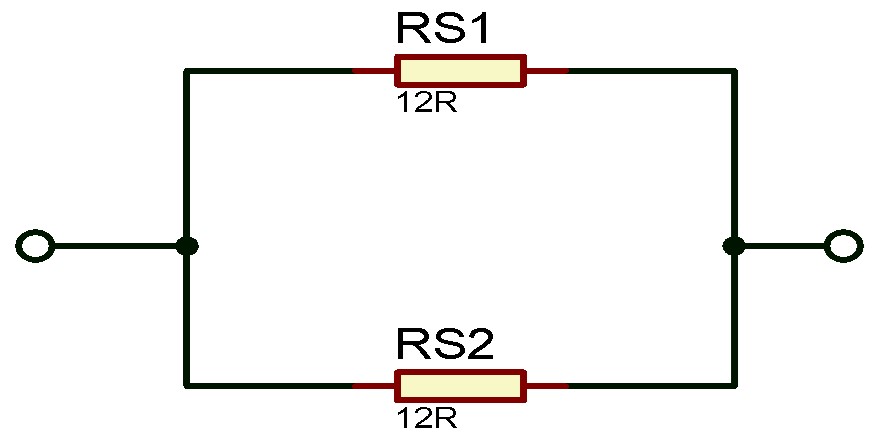
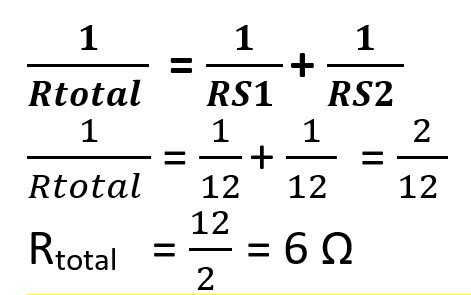
#Jadi, besar hambatan pengganti pada susunan itu adalah 6Ω.