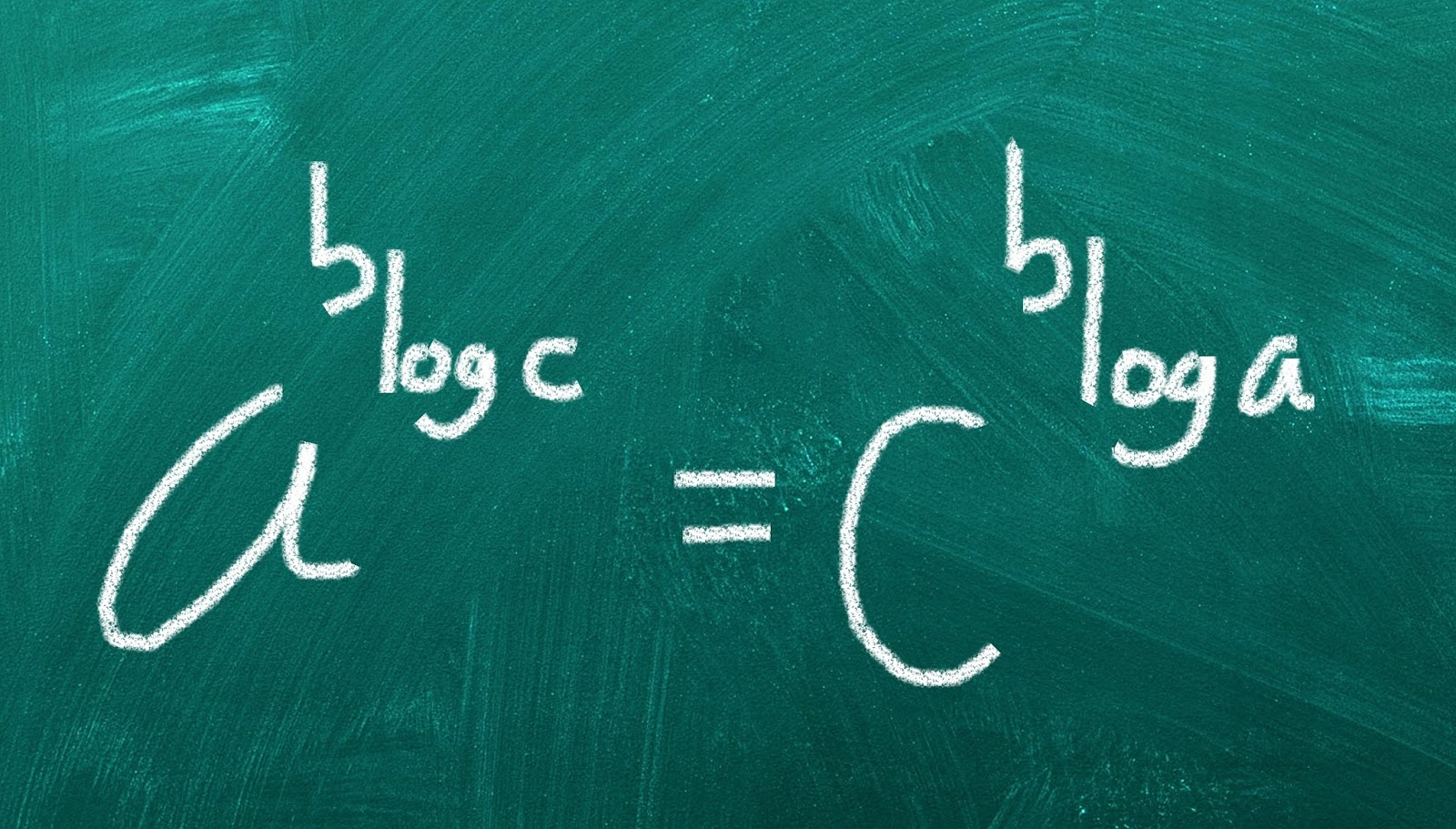Logaritma merupakan materi penting dalam Matematika yang merupakan kebalikan atau invers dari pemangkatan. Perhitungan menggunakan sifat-sifat logaritma sebenarnya banyak dimanfaatkan dalam kehidupan seperti ilmu antropologi pengukuran usia fosil, keuangan dan lainnya.
Banyak pelajar menganggap ilmu logaritma seperti momok yang menakutkan. Padahal, perhitungan dengan logaritma sebenarnya tidak sulit selama Anda mengetahui sifat dan cara perhitungannya. Pada artikel ini akan dibahas sifat logaritma beserta contohnya lengkap.
Pengertian Logaritma
Konsep logaritma diambil dari kebalikan atau invers materi pemangkatan atau eksponen matematika. Ilmu logaritma dikembangkan oleh seorang ahli Matematika berkebangsaan Inggris bernama John Napier di tahun 1614. Arti logaritma dalam bahasa Latin Tengah yaitu rasio bilangan.
Persamaan logaritma dituliskan menggunakan simbol “log”. Persamaan logaritma yang dituliskan alog b = c dalam persamaan eksponennya dituliskan sebagai ac = b dengan variabel a serta b merupakan bilangan real dimana a dan b > 0 sementara variabel c merupakan bilangan rasional.
Penulisan sederhana persamaan logaritma sebagai berikut:
rlog p = q
Keterangan:
r = basis atau bilangan pokok dengan nilai tidak boleh sama dengan 0 dan 1. Rentang nilai variabel a bisa dituliskan sebagai 0 < r < 1 dan r > 1
p = numerus atau bilangan yang dilogaritmakan dengan nilai p harus lebih dari 0 (p > 0)
q = hasil dari logaritma
Kegunaan Materi Logaritma di Kehidupan Sehari-Hari
Materi logaritma diterapkan dalam berbagai bidang kehidupan seperti cabang ilmu Fisika, ilmu akuntansi untuk menghitung besar bunga majemuk, menghitung besar inflasi dalam ilmu ekonomi, laju pertumbuhan penduduk, pengukuran usia fosil dalam ilmu antropologi.
Pada bidang Fisika misalnya, ilmu logaritma dipakai untuk menghitung skala bunyi dalam satuan decibel. Persamaan perhitungan skala bunyi dirumuskan oleh Alexander Graham Bell sebagai berikut D = 10 log I/I0.
Variabel D adalah skala decibel bunyi yang dicari. I0 merupakan batas intensitas bunyi terendah yang masih dapat didengar telinga manusia normal dengan nilai sebesar 1,0 x 10ˉ¹². Sementara I adalah intensitas bunyi yang dinyatakan dalam satuan Watt/m².
Sifat-Sifat Logaritma
Berdasarkan definisi dasar logaritma, maka bisa ditarik beberapa sifat logaritma. Dari sifat tersebut dibagi ke dalam beberapa kelompok seperti sifat dasar logaritma dan sifat operasi logaritma. Berikut adalah penjelasan dari masing-masing sifat-sifat logaritma:
- Sifat rlog r = 1, dengan r merupakan bilangan real yang nilainya lebih dari 0 (r > 0) dan tidak sama dengan 1
- Apabila a dan b merupakan bilangan real, yang mana bilangan a > 0 dan a ≠ 1, sehingga berlaku padanya:
- Sifat rlog 1 = 0, dengan r > 0, r tidak sama dengan 1, dan r merupakan bilangan real
- Sifat rlog rn = n, dengan r > 0, r ≠ 1, variabel r dan n merupakan bilangan real
- Persamaan logaritma berlaku sifat rlog (p x q) = rlog p + rlog q jika bilangan r, p, q merupakan bilangan real positif dengan variabel r ≠ 1 sementara variabel p > 0.
- Sifat operasi logaritma berlaku rlog (p/q) = rlog p – rlog q, dengan syarat variabel r dan p merupakan bilangan real positif, r > 0 dan r ≠ 1, p > 0
- Sifat operasi logaritma berlaku rlog pn = n rlog p dimana variabel r, p dan n merupakan bilangan asli dengan nilai r > 0, p > 0, dan r ≠ 1
- Sifat operasi logaritma berlaku rlog p = qlog p/ qlog r = 1/plog r, dimana variabel r, p dan q merupakan bilangan real positif, dengan nilai variabel r ≠ 1, p ≠ 1, dan q ≠ 1.
- Sifat operasi logaritma berlaku rlog p x plog q = rlog q, dimana variabel r, p dan q merupakan bilangan real positif, dengan nilai variabel r ≠ 1 dan p ≠ 1
- Sifat operasi logaritma berlaku r^mlog pn = n/m (rlog p), dimana variabel r dan p adalah bilangan real positif, dengan nilai variabel r ≠ 1, sementara m dan n merupakan bilangan rasional dengan nilai m ≠ 0.
- Sifat operasi logaritma berlaku = p, dimana variabel r dan p adalah bilangan real positif, dengan nilai variabel r ≠ 1
- Sifat operasi logaritma berlaku rlog (p/q) = – rlog (q/p)
- Sifat operasi logaritma berlaku rlog q = rlog p x plog s x slog q
Kumpulan Soal Logaritma dan Jawabannya
Agar Anda lebih terbiasa mengerjakan soal yang melibatkan logaritma, berikut ini adalah beberapa contoh soal logaritma yang biasa keluar di ujian. Soal sudah dilengkapi dengan jawaban penjelasan untuk mengasah kemampuan.
1. Contoh 1
Hitunglah berapakah jawaban dari soal logaritma sederhana di bawah ini:
²log 128
³log 81
Jawab:
²log 128
= ²log 2⁷
= 7. ²log 2
= 7.1
= 7
³log 81
= ³log 3⁴
= 4. ³log 3
= 4
2. Contoh 2
Hitunglah jawaban dari soal di bawah ini:
⁵log 100 – ⁵log 4
³log 9 + ³log 81
Jawab:
⁵log 100 – ⁵log 4
= ⁵log (100/4)
= ⁵log 25
= ⁵log 5²
= 2. ⁵log 5
= 2.1 = 2
³log 9 + ³log 81
= ³log 3² + ³log 3⁴
= 2. ³log 3 + 4. ³log 3
= 2.1 + 4.1
= 6
3. Contoh 3
Jika diketahui nilai ⁷log 2 = p dan ²log 3 = q maka tentukanlah berapa nilai dari ⁹log 7 menggunakan variabel p dan q
Jawab:
Pertama-tama bentuk dari logaritma ⁷log 2 diubah menjadi ²log 7 menggunakan sifat-sifat logaritma seperti di bawah ini:
⁷log 2 = p
log 2/ log 7 = p
log 7/ log 2 = 1/p
²log 7 = 1/p
Nilai dari ⁹log 7 bisa dihitung menggunakan cara berikut ini:
⁹log 7
= log 7/ log 9
= ²log 7/ ²log 9
= ²log 7/ ²log 3²
= ²log 7/ (2 x ²log 3)
= 1/p : (2 x q)
4. Contoh 4
Tentukan berapakah hasil dari persamaan logaritma berikut: ²log 100 + ⁵log 500 – ²log 25 – ⁵log 4
Jawab:
Untuk menyelesaikan soal logaritma di atas menggunakan sifat dari operasi hitung logaritma dimana tanda (+) untuk indeks seragam artinya kali sementara (-) artinya dibagi.
²log 100 – ²log 25 + ⁵log 500 – ⁵log 4
= ²log (100/25) + ⁵log (500/4)
= ²log 4 + ⁵log 125
= ²log 2² + ⁵log 5³
= 2 + 3 = 5
Logaritma adalah kebalikan atau invers dari perpangkatan atau eksponen yang dinyatakan dengan “log”. Agar bisa menyelesaikan persamaan yang melibatkan logaritma, maka modal yang harus dikuasai adalah sifat-sifat logaritma.