Inferensial adalah salah satu cara untuk menganalisis data yang saat ini karena memang banyak penelitian yang melibatkan sebuah populasi. Saat akan melakukan proses analisis data, maka metode yang digunakan harus sesuai.
Dalam artikel ini akan dibahas secara lengkap mengenai statistik inferensial mulai dari pengertian, jenis, fungsi hingga perbedaanya dengan statistik deskriptif. Simak pembahasan lengkapnya sampai akhir artikel!
Pengertian Statistik Inferensial Adalah
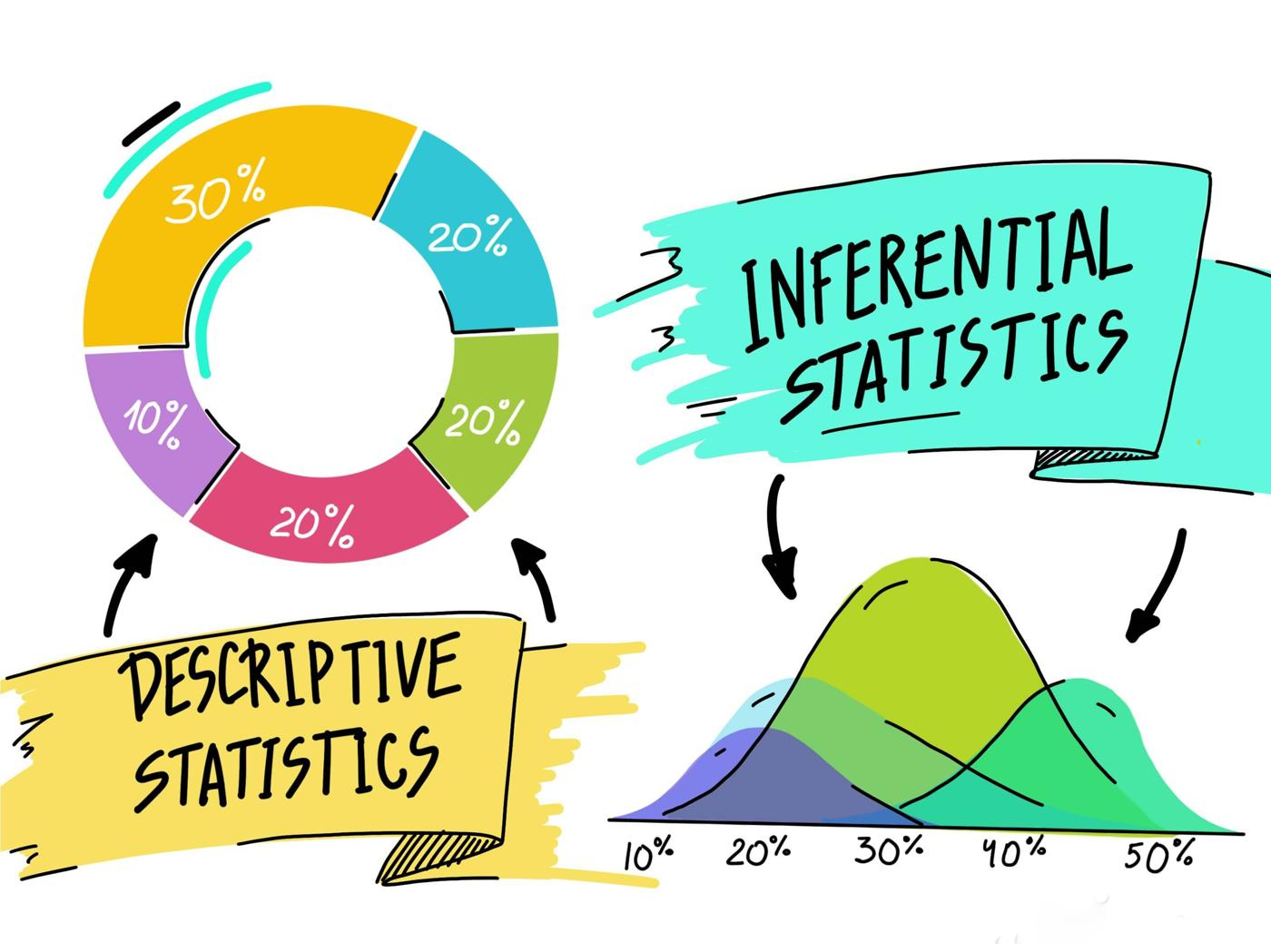
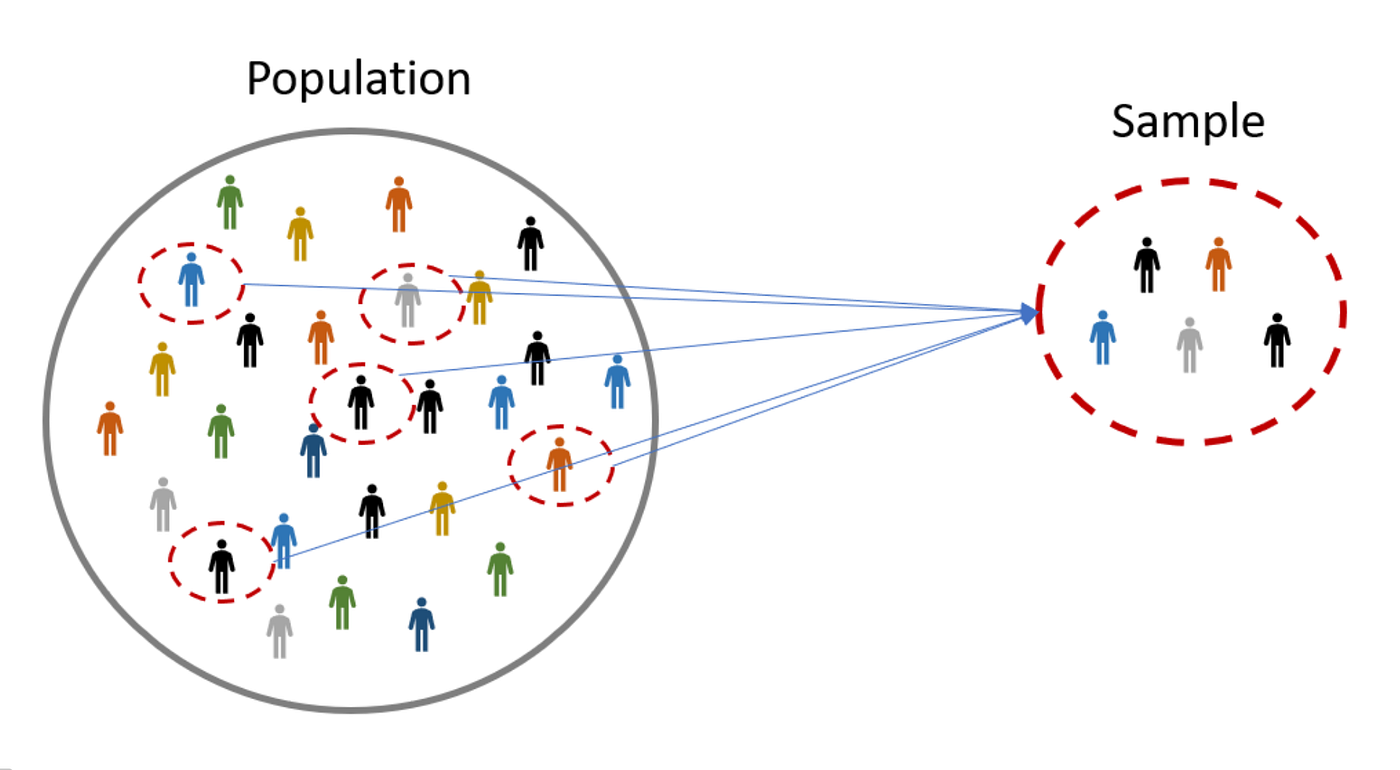
Statistik inferensial adalah sebuah teknik untuk menganalisis data yang digunakan untuk mengetahui sejauh mana adanya kesamaan antara hasil yang diperoleh dari sebuah penelitian dari suatu sampel dengan hasil yang diperoleh dari keseluruhan populasi yang diteliti.
Jadi, tujuan melakukan perhitungan statistik inferensial yakni untuk membantu peneliti dalam mencari tahu apakah hasil penelitian yang diperoleh dari suatu sampel bisa mewakili atau digeneralisasikan sebuah populasi.
Berikut ini beberapa pengertian mengenai statistik inferensial yang dikemukakan oleh para ahli, diantaranya adalah:
- Menurut Bartolucci dan Scrucca, statistik inferensial merupakan statistik yang berhubungan dengan menyimpulkan tentang sebuah parameter yang menggambarkan distribusi semua variabel yang ada dalam populasi tertentu berdasarkan sampel acak yang diteliti oleh peneliti.
- Menurut Subana, statistik inferensial merupakan metode analisis yang berhubungan dengan penarikan sebuah kesimpulan yang memiliki sifat general dari data yang diperoleh selama di lapangan.
- Menurut Walpole, statistik inferensial merupakan metode analisis yang berhubungan dengan analisis sebagian data penelitian yang sudah diperoleh untuk penarikan kesimpulan atau peramalan dari keseluruhan populasi.
Fungsi Statistika Inferensial
Statistika inferensial juga banyak disebut dengan statistika induktif karena memiliki fungsi diantaranya adalah:
- Untuk melakukan generalisasi yang datanya hanya dari sampel untuk mewakili sebuah populasi
- Untuk melaksanakan uji hipotesis.
Metode Analisis dan Pengujian Statistik Inferensial
Setidaknya terdapat dua metode analisis utama dalam statistik inferensial yakni pengujian hipotesis dan estimasi parameter.
Pengujian hipotesis biasanya disebut dengan signifikansi melibatkan apakah ada perbedaan rata-rata dari kedua sampe secara signifikan. Sedangkan estimasi parameter menggunakan mode, median, mean, dan nilai deviasi standar dari suatu populasi.
Untuk melakukan pengujian dalam statistik inferensial, metode pengujian yang biasa digunakan diantaranya adalah:
1. Analisis Varians
Metode analisis yang satu ini digunakan untuk menguji dan menganalisis perbedaan mean dari dua atau lebih kumpulan data.
2. Analisis Korelasi
Metode analisis yang satu ini digunakan untuk menguji sejauh mana korelasi antar dua variabel. Dengan menggunakan uji ini, peneliti dapat melihat apakah variabel yang ada pada penelitian tersebut memiliki korelasi yang kuat atau lemah.
3. Analisis Regresi Linier
Metode analisis yang satu ini digunakan untuk mengetahui hubungan antara dua variabel dalam penelitian. Lebih tepatnya adalah untuk mengetahui bagaimana pengaruh dari satu atau lebih variabel independen terhadap satu variabel dependen.
4. Uji-T
Metode analisis yang satu ini digunakan untuk membandingkan rata-rata dari dua kelompok dan mencari perbedaannya.
Jenis-Jenis Statistika Inferensial
Dalam statistika inferensial adalah terdapat dua jenis yakni parametrik dan non parametrik. Berikut pembahasan lengkapnya mengenai kedua jenis dalam statistik inferensial tersebut.
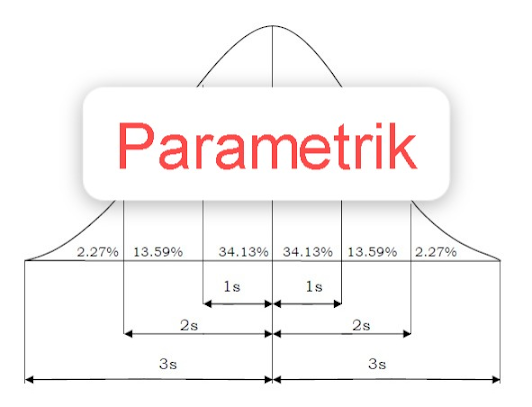
1. Statistik Parametrik
Statistik parametrik merupakan sebuah uji hipotesis yang menguji dengan perbedaan rata-rata pada sebuah populasi. Metode yang paling sering digunakan untuk menguji statistik parametrik adalah uji-t, unpaired t-test, paired t-test, pearson correlation dan ANOVA.
2. Statistik Non Parametrik
Statistik non parametrik merupakan uji yang tidak memerlukan asumsi parameter apapun untuk mewakili populasi yang diuji. Jika dalam bahasa sederhananya, tidak ada parameter yang digunakan atau tidak ada distribusi sampel yang perlu diketahui.
Sehingga statistik ini sering disebut juga sebagai metode bebas distribusi. Dalam perhitungan statistik non parametrik, variabel-variabel yang ada akan diukur dengan skala ordinal dan nominal.
Metode yang biasa digunakan dalam statistik non parametrik biasanya adalah mann whitney u-test, kruskal wallis test, spearman correlation dan wilcoxon rank sum test.
3. Statistik Univariat
Statistik univariat digunakan jika hanya terdapat satu variabel saja yang diukur untuk satu sampel. Statistik univariat juga digunakan jika ada beberapa variabel tetapi masing-masing dari variabel penelitian tersebut diteliti sendiri-sendiri tanpa ada hubungan antara satu dengan lainnya.
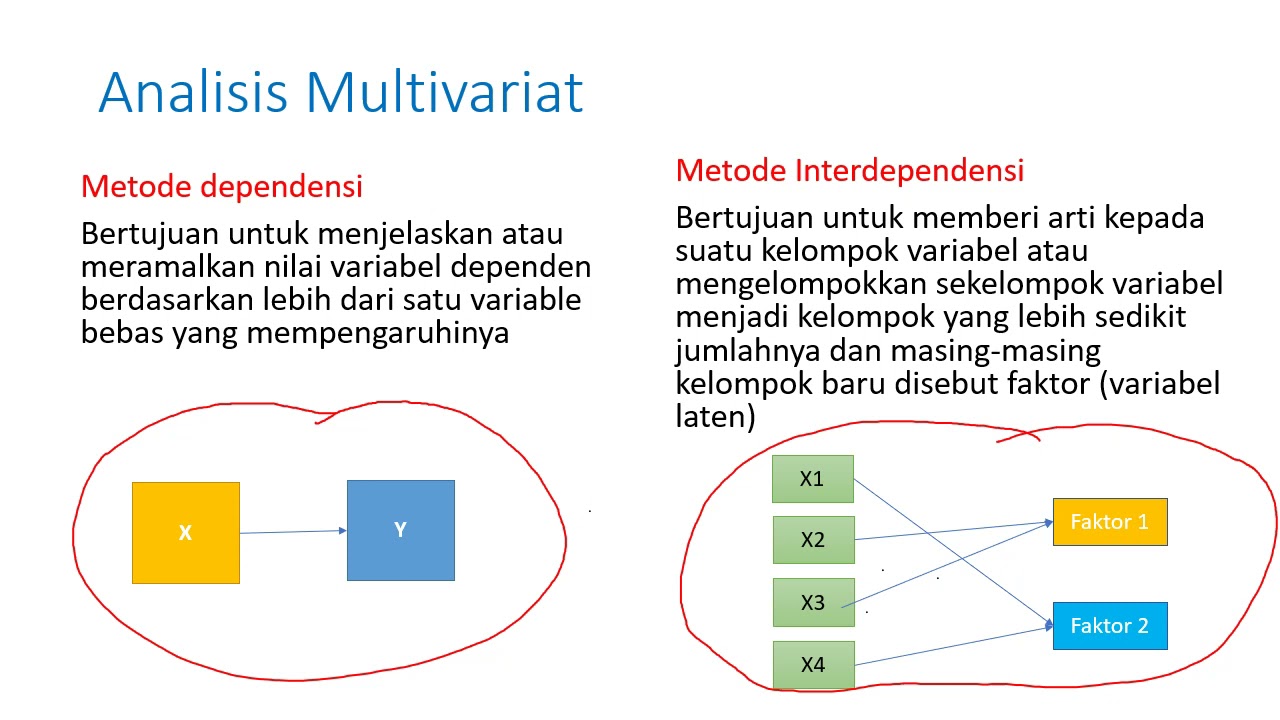
4. Statistik Multivariat
Statistik multivariat jika terdapat dua atau lebih variabel yang diukur untuk satu sampel dan semua variabel dianalisis secara bersama-sama.Statistik jenis ini merupakan salah satu teknik statistik yang digunakan untuk memahami struktur data dalam jumlah yang banyak.
Statistik multivariat memiliki cara perhitungan yang sangat kompleks karena datanya yang sangat banyak. Sehingga tidak banyak peneliti menggunakan statistik multivariat dalam sebuah penelitian kuantitatif.
Namun, seiring berkembangnya zaman, saat ini sudah ada aplikasi yang mempermudah perhitungan statistik multivariat yakni SPSS. Dalam aplikasi SPSS sudah tersedia alat yang bisa digunakan untuk menganalisis statistik multivariat.
Jadi, saat ini sudah banyak peneliti yang menggunakan statistik multivariat untuk memahami secara lebih dalam mengenai data yang berjumlah banyak karena perhitungannya sudah sangat mudah menggunakan aplikasi.
Contoh Statistik Inferensial
Statistik inferensial banyak digunakan untuk menghitung sesuatu di kehidupan sehari-hari, berikut beberapa contoh penggunaan statistik inferensial, yakni:
1. Menghitung Berat Rata-Rata Warga di Suatu WIlayah
Apabila seorang peneliti ingin melakukan penelitian terkait berat rata-rata orang dewasa di suatu wilayah, maka tidak akan mungkin semua orang dewasa di wilayah tersebut diukur satu per satu karena tidak praktis dan akan memerlukan tenaga yang sangat banyak dan waktu yang lama.
Maka, disinilah peneliti bisa menggunakan statistik inferensial untuk menentukan perkiraan berat rata-rata orang dewasa di wilayah tersebut. Nilai akhir yang dihasilkan dari perhitungan statistik inferensial nantinya akan bergantung pada pengumpulan data sampel individu ketika di lapangan.
Selanjutnya peneliti akan mengukur berat badan sampel yang ditentukan secara acak dengan syarat wajib adalah orang dewasa. Setelah melakukan pengambilan berat badan dari sampel, maka akan masuk ke dalam analisis statistik inferensial dengan menggunakan berbagai metode uji diatas.
Setelah ketemu hasil dan melakukan uji hipotesis, maka peneliti akan menemukan jawaban mengenai perkiraan rata-rata berat badan orang dewasa di wilayah tersebut secara general karena data dari sampel digeneralisasikan untuk mewakili populasi yang ada.
2. Mencatat Kelulusan
Jika sebuah SMA memiliki catatan kelulusan selama lima tahun terakhir adalah sekitar 73% siswa dan siswinya dapat lulus dengan capaian yang memuaskan, maka Anda bisa meramalkan bahwa seorang siswa atau siswi saat ini dapat lulus dengan nilai memuaskan sebesar 70%.
Mengapa demikian? Karena data sampel yakni data kelulusan lima tahun lalu menunjukkan angka 73% dimana bisa dijadikan data peramalan untuk tahun-tahun lainnya terkait dengan kelulusan siswa atau siswi SMA tersebut.
Memahami secara lengkap dan mendalam mengenai inferensial adalah langkah yang harus diambil pertama kali. Apalagi untuk Anda yang akan melakukan penelitian kuantitatif dan yang berhubungan dengan pengaruh satu atau lebih variabel independen terhadap satu variabel dependen.
Dengan menggunakan statistik inferensial, Anda akan lebih mudah dalam menentukan peramalan atau menarik kesimpulan. Hal ini karena hanya perlu mengumpulkan data dari beberapa sampel untuk mewakili suatu populasi.