Dalam dunia matematika, terdapat konsep nilai mutlak yang biasanya dikenal dengan nilai positif seperti ketika melakukan penghitungan jarak. Saat menghitung jarak suatu tempat ke tempat lain, maka nilainya pasti positif, tidak pernah minus.
Penggunaan konsep matematika satu ini juga beragam, seperti menghitung kecepatan, suhu, ketinggian, sampai penghitungan biaya. Dengan demikian, dapat dipahami sebagai konsep yang tidak akan pernah ditemui nilai negatif di dalamnya.
Pada mata pelajaran matematika, Anda akan menemui materi nilai mutlak dan menerapkan berbagai jenis contoh soal. Agar lebih memudahkan dalam memahami dan memecahkan soal, simak penjelasan tentang pengertian serta sifat nilai mutlak berikut ini.
Pengertian Nilai Mutlak
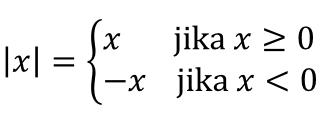
Mutlak matematika adalah sebuah konsep yang mendefinisikan angka dari nol dengan bilangan positif tanpa melihat arahnya. Ini kemudian dipahami lebih sederhana sebagai konsep nilai absolut atau jarak sebenarnya jika bilangan dilihat dari titik nol pada garis bilangan.
Nilai absolut ini mempunyai angka-angka riil tanpa tanda tambah (+) atau kurang (-). Hal tersebut dapat dilihat pada suatu garis bilangan dimana jika bergerak kearah kanan akan menuju nilai positif (+) dan apabila ke arah kiri, maka nilainya negative (-).
Nilai mutlak secara simbolis dilambangkan atau dinotasikan dengan |x| (dibaca: nilai mutlak x). Sementara itu, dalam definisi matematika, didefinisikan dengan x jika x ≥ 0 dan –x jika x < 0.
Agar lebih jelas, rumus dapat dilihat seperti di bawah ini.
|x|
x, jika x ≥ 0
-x, jika x < 0
Rumus di atas dipahami seperti berikut:
- Nilai mutlak positif (+) atau nol adalah bilangan itu sendiri
- Nilai mutlak negative (-) adalah lawan dari bilangan negatif tersebut
Dari penjelasan rumus tersebut, maka dapat ditemukan contoh soal mutlak misalkan sebagai berikut.
- |9| = 9, karena 9 > 0 (9 merupakan bilangan positif)
- |-6| = -(-6) = 6, karena -4 < 0 (-4 merupakan bilangan negatif)
Sifat Nilai Mutlak

Sifat mutlak artinya nilai suatu bilangan dimana selalu dinyatakan positif atau nol. Dalam matematika, konsep ini mempunyai sifat-sifat seperti berikut.
|α| ≥ 0
Sifat pertama adalah simbol |α| ≥ 0 dimana nilai absoutnya dibaca “nilai mutlak a selalu lebih besar atau sama dengan nol”. Ini juga dapat dipahami bahwa nilainya selalu positif atau tidak mungkin bernilai negative atau minus.
|-α| = |α|
Pada konsep berikutnya mempunyai sifat yang dibaca “nilai mutlak dari –a sama dengan nilai mutlak dari a itu sendiri”. Maksudnya adalah ketika bilangan memiliki nilai yang negatif, maka nilai absolutnya adalah kebalikan dari bilangan tersebut sehingga –a sama dengan a.
|α| = √α2
Sifat persamaan ini dibaca “nilai mutlak dari a sama dengan akar kuadrat dari a pangkat dua”. Dalam mencari pangkat √α2 harus menemukan hasil α2 atau (-α2) contohnya adalah 72 atau (-72) yaitu 49, maka √49 atau √72 sama dengan 7 atau -7 (simbolnya |α|
|α.b|= |α|.|b|
Sifat mutlak selanjutnya menunjukkan hasil perkalian dari dua bilangan yang sama dengan hasil kali dari nilai absolut masing-masing bilangan tersebut. Contohnya adalah sebagai berikut.
|α.b|= |α|.|b|
|4. (-5)| = |4|. (-5)|
|-20| = 4.5 = 20
|α/b|= (|α|)/(|b|, b ≠ 0
Dalam mencari nilai mutlak pembagian dua bilangan, harus membagi kemudian mengubahnya jadi bentuk yang absolut. Selain itu, juga dapat mengubah menjadi mutlak lalu baru membaginya, namun perlu diingat jika sifat ini berlaku apabila nilai b mutlak tidak sama dengan 0.
Grafik Fungsi
Agar lebih mudah dalam memahami nilai absolut, maka dapat melihat grafiknya. Fungsi mutlak pada grafik bisa ditemukan dengan beberapa langkah berikut.
- Buatlah tabel fungsi dari nilai absolut menggunakan titik bantu
- Isi tabel fungsi sesuai definisi nilai absolut
- Isi dan sajikan titik-titik yang didapatkan dengan memakai cara koordinat kartesius
Contoh Nilai Mutlak
Penerapan nilai mutlak dapat ditemukan dengan mudah dalam kehidupan sehari-hari di berbagai aspek. Berikut adalah sejumlah penerapan yang paling umum terjadi atau memakai konsep nilai absolut ini.
1. Umur
Dari mulai kelahiran manusia atau makhluk hidup lainnya akan dihitung dari nilai positif, meskipun masih di dalam kandungan tidak akan disebut dengan -1 bulan. Umur akan selalu dihitung serta bernilai positif (tidak mungkin nilainya menjadi negative (-)).
2. Jarak
Menghitung jarak dari suatu tempat ke tempat lainnya juga menggunakan konsep matematika berupa kemutlakan nilai, seperti jarak dari rumah ke pasar adalah 5 meter. Tidak akan mungkin nilai dari jarak adalah -5 meter.
3. Biaya
Penerapan dari penggunaan nilai absolut berikutnya adalah pada penghitungan biaya, misalkan harga pembayaran tagihan listrik bulan Maret adalah Rp165.000. Nilainya akan selalu positif sehingga tidak akan ditemukan biaya dengan nilai –Rp165.000.
Tidak hanya penerapan pada penghitungan umur, jarak, dan biaya saja. Beberapa fenomena lain seperti menghitung ketinggian, kedalaman, kecepatan, langkah, dan sejenisnya juga memakai konsep nilai absolut ini.
Contoh Soal Penyelesaian Himpunan

Terdapat sejumlah soal yang terkait dengan penggunaan nilai mutlak, salah satunya adalah penyelesaian himpunan. Himpunan sendiri merupakan materi yang masuk ke dalam persamaan dan pertidaksamaan.
Adapun beberapa contoh soal dan pembahasannya adalah seperti berikut ini.
1. Himpunan penyelesaian dari 2x 7 5
Soal ini juga dapat dipahami dengan |2x-7| = 5. Dengan demikian, penjabaran pembahasannya adalah sebagai berikut.
Nilai x yang dapat memenuhi persamaan |2x-7| = 5 adalah 1 dan 6.
Untuk x>0
2x-7= 5
2x= 5 + 7
2x = 12
X=12:2
X= 6
Untuk x<0
-(2x-7)= 5
-2x + 7 = 5
-2x = 5-7
-2x= -2
X = -2 : -2
X= 1
Himpunan penyelesaian dari 2x 7 5 adalah HP = {1,6}
2. Himpunan penyelesaian dari 2x 1 7
Soal |2x-1|=7 dapat diselesaikan dengan langkah-langkah seperti di bawah ini.
Cara Penyelesaian 1
2x -1 = 7
2x = 7+1
2x = 8
X= 8:2
X= 4
Cara Penyelesaian 2
2x – 1 = -7
2x = -7 + 1
2x = -6
X = -6:2
X= -3
Himpunan penyelesaian dari 2x 1 7 yaitu HP = {-3, 4)
3. Himpunan penyelesaian dari 2x 7 3
Contoh soal berikutnya dapat diselesaikan dengan langkah seperti di bawah ini.
Jika |2x-7| = 3, maka 2x-7 = 3 atau 2x -7 = -3
2x=3+7 2x=-3+7
2x=10 2x=4
X=10/2 x=4/2
X= 5 x= 2
Jadi, himpunan penyelesaian dari 2x 7 3 adalah HP={2,5}.
Melalui pembahasan nilai absolut ini, maka dapat dipahami bahwa nilai yang bersifat mutlak adalah absolut atau sudah pasti akan selalu positif. Hal tersebut dapat dilihat dari sejumlah penerapan penghitungan, mulai dari umur, jarak, biaya, kedalaman, ketinggian, dan lainnya.
Penerapan ini juga melibatkan penyelesaian soal-soal, termasuk himpunan yang bisa dicari nilainya dengan melihat dua kemungkinan, yaitu x>0 dan x<0.