Sistem bilangan komputer merupakan sebuah cara yang digunakan untuk mewakili bilangan dengan simbol yang sudah disepakati atau sesuai standar. Fungsi sistem bilangan pada komputer mulanya digunakan sebagai bentuk konversi untuk tegangan menjadi data, selain itu sistem bilangan mempunyai tujuan untuk mengubah data analog menjadi data digital. Sistem bilangan sendiri mempunyai 4 jenis yaitu bilangan desimal, bilangan biner, bilangan octal, dan bilangan heksadesimal. Pada artikel kali ini kita akan belajar tentang bilangan desimal dan cara konversinya.
Pengertian Bilangan Desimal
Bilangan desimal adalah sistem bilangan yang menggunakan baris / radix 10. Kata desimal diperoleh dari kata latin decem yang artinya sepuluh. Bilangan desimal terdiri dari 10 angka yaitu: 0,1,2,3,4,5,6,7,8, dan 9. Dalam bilangan desimal terdapat dua istilah yaitu Most Significant Digit (MSD) dan Least Significant Digit (LSD).
- Most Significant Digit (MSD) yaitu digit yang bertindak menjadi digit terbesar.
- Least Significant Digit (LSD) yaitu digit yang mempunyai nilai terkecil.
Contoh bilangan desimal adalah 345. Pada bilangan ini angka 3 merupakan MSD atau digit yang mempunyai nilai terbesar sebagai ratusan, angka 4 sebagai puluhan dan angka 5 sebagai LSD atau nilai terkecil berarti satuan.
345 = (3 x 102) + (4 x 101) + (5 x 100) = 300 + 40 + 5 = 345.
Cara Konversi Bilangan Desimal
Untuk melakukan konversi bilangan desimal ke sistem bilangan lain ataupun sebaliknya dari sistem bilangan lain ke sistem bilangan desimal cukup mudah, hanya perlu mengkalikan atau membagi dengan bilangan radix yang dituju. Misal radix bilangan oktal adalah 8, radix bilangan biner adalah 2 dan radix bilangan heksadesimal adalah 16. Penjelasan lebih lengkap akan dijelaskan persubab berdasarkan jenis sistem bilangannya.
A. Penulisan Sistem Bilangan
Untuk cara menulis sistem bilangan adalah dengan menambahkan tanda kurung di akhir bilangannya, berikut adalah contoh penulisan dari sistem bilangan.
Bilangan Biner 1011 1110 (2)
Bilangan Oktal 17 (8)
Bilangan Heksadesimal A4 (16)
Bilangan Desimal 101 (10)
B. Konversi Bilangan Desimal ke Biner
Untuk melakukan konversi dari bilangan desimal ke biner konsep utamanya adalah membagi bilangan desimal dengan basis bilangan tujuan seperti bilangan biner adalah 2. Semua bilangan desimal dibagi 2 kemudian menyimpan sisa pembagiannya sampai hasil baginya kurang dari 2. Cara membaca hasil konversinya adalah dari urutan sis bagi yang paling akhir sampai ke bagian awal. Sederhananya perhatikan contoh berikut ini:
57(10) = …. (2)
| Pembagi | Hasil Bagi | Sisa bagi |
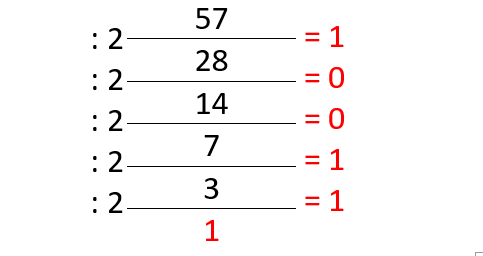
Jadi bilangan biner dari 57(10) = 111001(2)
C. Konversi Bilangan Biner ke Desimal
Cara konversi bilangan biner ke desimal cukup mudah, tinggal mengalikan bilangan satu persatu dengan radix biner yaitu 2 pangkat 0,1, atau 2, dst. Lalu setelahnya tinggal dijumlahkan. Untuk lebih jelasnya perhatikan contoh soal berikut ini.
111001(2) = …. (10)
= (1 x 25) + (1 x 24) + (1 x 23) + (0 x 22) + (0 x 21) + (1 x 20) = 32+ 16 + 8 + 0 + 0 + 1 = 57
D. Konversi Bilangan Desimal ke Oktal
Konversi bilangan desimal ke oktal dengan cara bilangan desimal dibagi dengan 8 dan menyimpan sisa bagi tiap bagiannya sampai hasil bagi kurang dari 8. Hasil konversi diurutkan dari yang terakhir sampai ke awal. Berikut adalah contoh konversi bilangannya.
87(10) = ….. (8)
| Pembagi | Hasil Bagi | Sisa bagi |
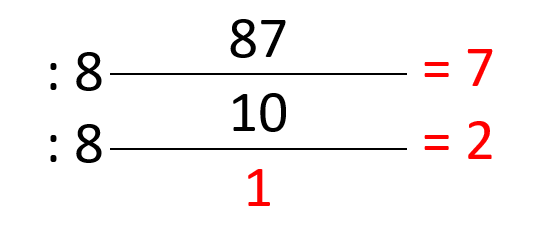
Jadi bilangan oktal dari 87(10) = 127(8)
E. Konversi Bilangan Oktal ke Desimal
Konversi bilangan dari oktal ke desimal yaitu dengan cara mengalikan bilangan satu persatu dengan baris oktal yaitu 8 pangkat 0,1, atau 2, dst. Perkalian ini dimulai dari kanan ke kiri, kemudian hasil perkalian tersebut dijumlahkan. Contohnya 127(8) berapakah nilai desimalnya?
127(8) = …… (10)
= (1 x 82) + (2 x 81) + (7 x 80) = 64 + 16 + 7 = 87(10)
F. Konversi Bilangan Desimal ke Heksadesimal
Konversi bilangan desimal ke heksadesimal dapat dilakukan dengan cara bilangan desimal dibagi dengan 16 dan simpan sisa baginya tiap bagian hingga hasil baginya kurang dari 16. Cara membaca hasil konversinya dari yang paling akhir sampai ke bagian awal. Perlu diketahui pada bilangan heksadesimal hanya sampai angka 9, jika lebih dari itu angkanya perlu diganti dengan huruf. Nilai bilangan 10 adalah A, bilangan 11 adalah B, bilangan 12 adalah C, bilangan 13 adalah D, bilangan 14 adalah E, dan bilangan 15 adalah F. berikut adalah contoh cara melakukan konversi bilangan desimal ke heksa desimal.
8026(10) = ….. (16)
| Pembagi | Hasil Bagi | Sisa bagi |
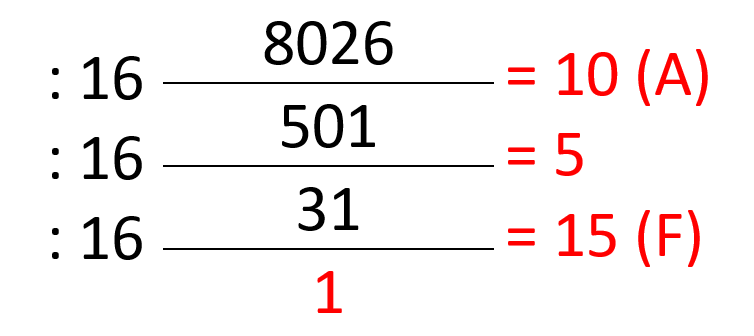
Jadi bilangan heksadesimal dari 8026(10) = 1F5A(16)
G. Konversi Bilangan Heksadesimal ke Desimal
Konversi bilangan heksadesimal ke desimal sama halnya dengan cara konversi bilangan lainnya yaitu dengan mengalikan angka satu persatu dengan radix heksadesimal yaitu 16. Perkalian dimulai dari kanan ke kiri dengan nilai pangkat mulai dari 0,1, atau 2, dst. Berikut contoh soal untuk mempermudah pemahaman Anda. Perlu diingat bahwa bilangan desimal terdapat huruf sebagai pengganti bilangan setelah 9, misalnya A = 10, B = 11, C = 12, D = 13, E = 14, dan F = 15.
1F5A(16) = …… (10)
= (1 x 163) + (15 x 162) + (5 x 161) + (10 x 160) = 4096 + 3840 + 80 + 10 = 8026(10)
Tak terasa sudah dipenghujung artikel, semoga materi ini bermanfaat bagi Anda dan sampai jumpa di artikel berikutnya. 😊