Sesuai dengan namanya, diagram panah merupakan diagram yang menunjukkan relasi antara anggota himpunan menggunakan simbol panah. Hal tersebut biasa ditemui pada relasi dan fungsi. Oleh karena itu, untuk memahami diagram tersebut, Anda perlu memahami betul tentang relasi dan juga fungsi.
Namun, Anda tidak perlu khawatir karena semua akan dibahas pada kali ini. Bahkan, untuk lebih memperkuat pemahaman, akan ada beberapa contoh soal yang kerap muncul terkait materi tersebut. Jadi, pastikan untuk menyimak hingga akhir.
Apa Itu Relasi?
Secara sederhana, dapat dikatakan bahwa relasi merupakan hubungan yang terdapat antara sebuah himpunan dari daerah asal dan kawan. Pada dunia matematika, daerah asal disebut dengan domain, sedangkan daerah kawan dinamakan kodomain.
Nantinya, anggota dari domain akan dipasangkan dengan anggota kodomain sesuai dengan relasi atau hubungannya. Sebagai contoh, terdapat himpunan A = {Jakarta, Seoul, Tokyo} dan B = {Indonesia, Korea Selatan, Jepang).
Dari kedua data tersebut, maka dapat dikatakan bahwa data tersebut saling berhubungan, yakni antara negara dengan ibukota. Apabila anggota domain masing-masing hanya memiliki satu pasangan maka akan disebut sebagai fungsi atau korespondensi satu-satu.
Untuk lebih jelas, terdapat himpunan A = {Indonesia, Korea Selatan} dan B = {nasi goreng, bulgogi, kimchi}. Dari data tersebut tidak dapat dikatakan fungsi karena terdapat anggota yang memiliki dua pasangan dari himpunan lain. Dalam kehidupan sehari-hari, Anda juga bisa menerapkan ini pada silsilah keluarga.
Diagram Panah untuk Menyatakan Relasi
Kebanyakan hubungan domain dengan kodomain akan dinyatakan dalam diagram panah. Meski begitu, sebenarnya masih ada beberapa alternatif metode lain untuk menyatakannya. Berikut adalah beberapa metode tersebut.
1. Menggunakan diagram panah
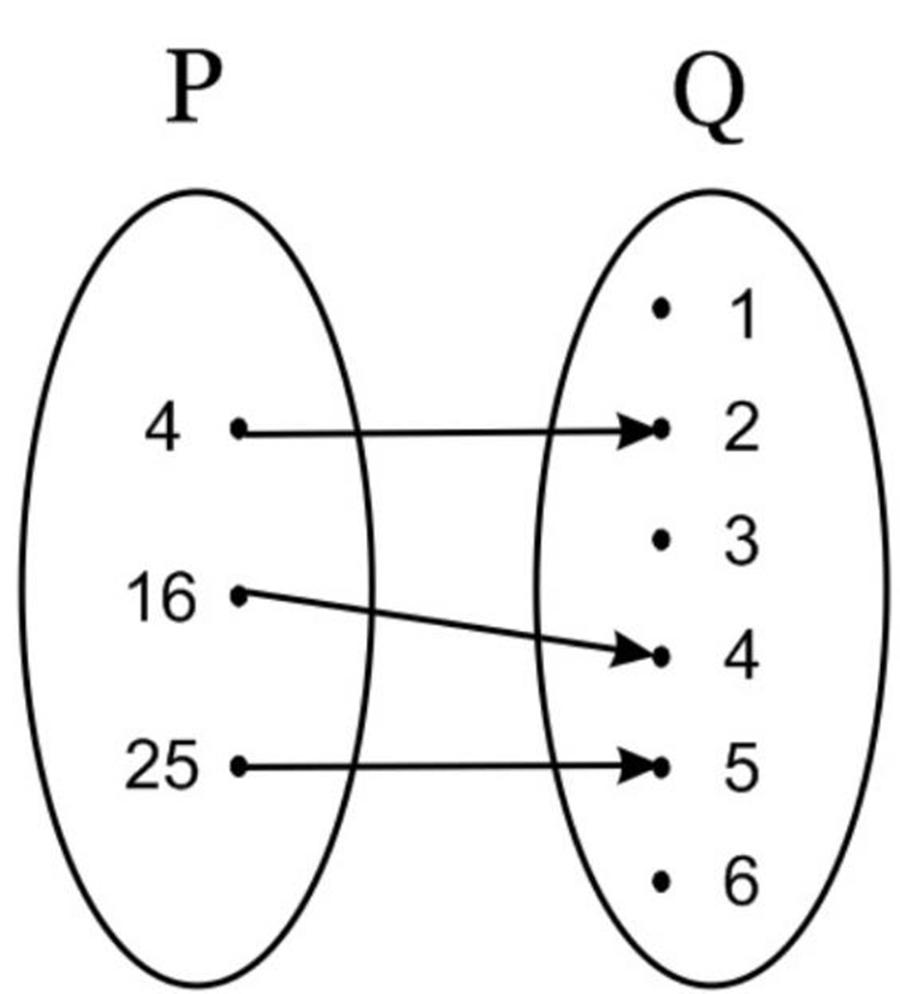
Seperti telah dijelaskan di bagian sebelumnya, diagram ini menggunakan tanda panah untuk menghubungkan anggota sebuah himpunan ke yang lain. Untuk menyatakan, Anda perlu membuat dua bangun sebagai daerah asal dan kawan. Setelah itu, berikan tanda titik sejumlah anggotanya. Hubungkan titik-titik dari domain ke daerah kawan menggunakan tanda panah.
Ketika setiap anggota hanya terhubung dengan satu panah dengan anggota lain di daerah kawan, maka panah ini akan menunjukkan sebuah relasi bernama pasangan berurutan. Akan tetapi, ketika satu anggota mempunyai dua pasangan kodomain, panah ini hanya disebut relasi saja.
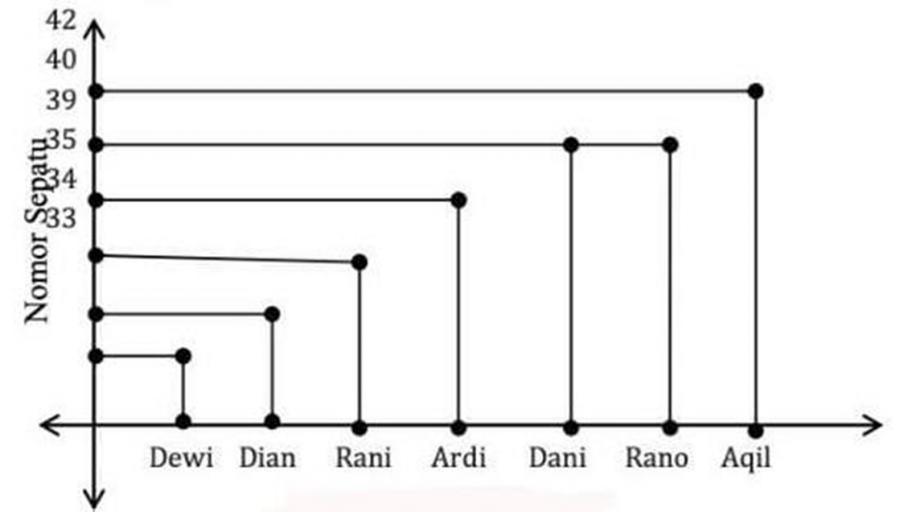
2. Diagram Cartesius
Selain diagram dengan tanda panah, ada satu lagi metode untuk menyatakan sebuah hubungan, yakni diagram cartesius. Bagi yang pernah belajar matematika mungkin sudah tidak asing lagi dengan istilah tersebut. Pada diagram cartesius, sumbu x akan menunjukkan domain, sedangkan sumbu y menunjukkan kodomain.
Apa Itu Fungsi?
Pada pembahasan awal, Anda sudah memahami bahwa sebuah hubungan akan disebut sebagai fungsi apabila setiap anggota domain hanya berpasangan dengan satu anggota daerah kawan saja. Dari hal tersebut, bisa dikatakan bahwa fungsi adalah sebuah relasi khusus dan fungsi sudah pasti sebuah relasi. Sebaliknya, relasi belum tentu merupakan fungsi. Beberapa syarat yang harus dipenuhi adalah sebagai berikut.
- Anggota domain tidak ada yang tidak berpasangan
- Semua anggota harus mempunyai pasangan di daerah lain
- Tidak ada anggota yang memiliki lebih dari satu pasangan
Jenis-Jenis Fungsi
Setidaknya terdapat tiga macam jenis diagram fungsi, yakni injektif, surjektif, dan bijektif. Berikut ini adalah penjelasan lengkap masing-masing jenisnya.
1. Injektif
Pertama adalah fungsi injektif, yakni sebuah fungsi dengan anggota daerah kawan yang hanya bisa berpasangan dengan satu anggota dari daerah asal saja. Pada jenis ini, anggota himpunan kawan tidak boleh tidak memiliki pasangan.
2. Surjektif
Berikutnya, ada istilah fungsi surjektif. Secara garis besar, istilah ini merupakan sebuah fungsi dengan anggota kawan tidak ada yang tidak berpasangan. Setiap anggota himpunan kawan boleh memiliki lebih dari satu pasangan dari himpunan asal.
3. Bijektif
Jenis yang terakhir adalah fungsi bijektif, yakni anggota kawan tidak boleh tidak memiliki pasangan. Kemudian, setiap anggota kawan harus mempunyai satu pasangan dari daerah asal. Maksudnya, anggota himpunan kawan tidak boleh bercabang.
4. Notasi fungsi
Untuk menuliskan sebuah fungsi, biasanya akan digunakan notasi f: A -> B, f (a) = b. Dari notasi ini, dapat dikatakan bahwa fungsi tersebut memetakan anggota dari himpunan A dengan anggota dari himpunan B.
Contoh Soal
Untuk memudahkan dalam memahami, mungkin Anda memerlukan beberapa contoh soal terkait materi di atas. Oleh karena itu, di sini ada contoh soal terkait dengan relasi dan fungsi. Pastikan untuk menyimaknya dengan baik.
1. Contoh soal 1
Perhatikan himpunan di bawah ini.
A = {(2,3), (3,4), (4,5), (5,6), (6,7)}
B = {(2,3), (2,4), (3,5), (4,7)}
C = {(1,3), (2,6), (3,9)}
Sebutkan himpunan yang merupakan fungsi!
Pembahasan:
Dalam menjawab pertanyaan di atas, Anda harus mengingat kembali apa saja syarat yang membuat relasi menjadi sebuah fungsi. Syarat tersebut antara lain setiap anggota himpunan asal memiliki tepat satu pasangan dari daerah kawan. Dari syarat di atas, maka dapat diperoleh data berikut.
Himpunan A
A = {(2,3), (3,4), (4,5), (5,6), (6,7)}
Domain = {2, 3, 4, 5, 6}
Kodomain = {3, 4, 5, 6, 7}
Relasi keduanya dapat dinyatakan dengan seperti ini:
2 -> 3
3 -> 4
4 -> 5
5 -> 6
6 -> 7
Oleh karena itu, himpunan A dapat dikatakan sebagai fungsi karena setiap anggota asal hanya memiliki satu pasangan saja dari daerah kawan.
Himpunan B
B = {(2,3), (2,4), (3,5), (4,7)}
Domain = {2, 3, 4}
Kodomain = {3, 4, 5, 7}
Relasi keduanya dapat dinyatakan dengan seperti ini:
2 -> 3
2 -> 4
3 -> 5
4 -> 7
Berdasarkan kedua syarat di atas, maka himpunan ini tidak termasuk fungsi karena terdapat anggota yang mempunyai dua pasangan dari himpunan kawan, yakni 2 -> 3, dan 2 -> 4.
Himpunan C
C = {(1,3), (2,6), (3,9)}
Domain = {1, 2, 3}
Kodomain = {3, 6, 9}
Relasi keduanya dapat dinyatakan dengan seperti ini:
1 -> 3
2 -> 6
3 -> 9
Dari data diatas, himpunan C termasuk fungsi karena masing-masing anggota mempunyai pasangan dan hanya satu pasangan saja. Oleh karena itu, jawaban atas pertanyaan di atas adalah himpunan A dan C.
2. Contoh soal 2
Terdapat himpunan A = {Manila, Jakarta, Tokyo} dan himpunan B = {Jepang, Filipina, Indonesia}. Relasi dari himpunan A ke B dinyatakan sebagai …
Jawaban atas pertanyaan tersebut adalah ibu kota. Hal tersebut terlihat dari himpunan A berisi nama-nama ibukota, sedangkan himpunan B berisi nama-nama negara.
Dari penjelasan di atas, bisa dikatakan bahwa relasi dan fungsi sebenarnya cukup sering ditemui di kehidupan sehari-hari. Untuk menyatakannya, Anda bisa menggunakan diagram panah maupun diagram cartesius sesuai dengan kebutuhan.
Masing-masing memiliki kelebihan dan kekurangan masing-masing. Sebagai contoh, diagram menggunakan panah memang cenderung lebih mudah untuk dibaca karena terdapat garis bantu untuk membaca hubungan antara daerah asal dan daerah kawan.