Tahukah Anda apa itu standar deviasi? Dalam pelajaran statistika, nilai standar tersebut termasuk di dalam nilai variabilitas dengan rumus tersendiri. Tapi, kalau dibandingkan nilai variabilitas lain nilai yang juga disebut simpangan baku ini lebih banyak digunakan.
Bukan saja ketika mempelajari statistika, tapi juga untuk pembuatan data di berbagai bidang kerja. Kalau sekarang Anda belum paham artinya, maka simak saja penjelasan lengkapnya berikut.
Pengertian Simpangan Baku
Nilai ini disebut dengan sebaran dari data sampel yang dimiliki, fungsinya untuk menentukan berapa kedekatan nilai data dan nilai rata-rata dari data sampel yang ada. Bisa juga dijelaskan sebagai akar kuadrat dari nilai varians, yang akan memperlihatkan penyimpangan data dengan nilai rata-rata yang ada.
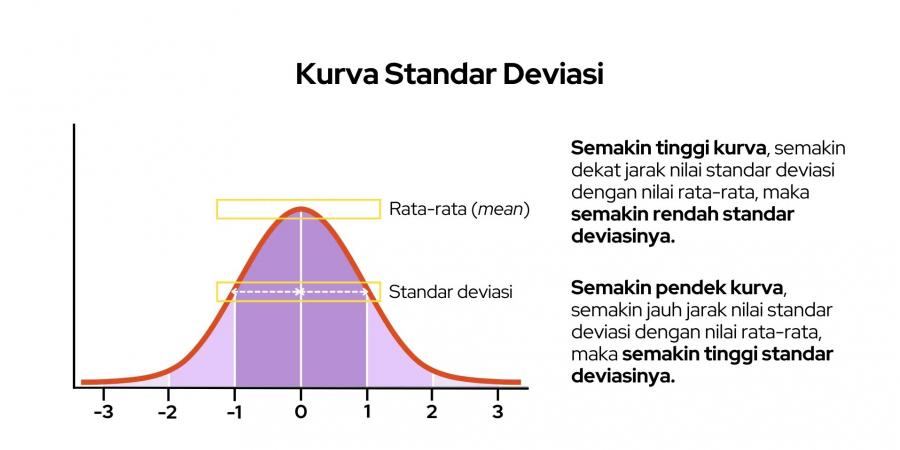
Kesimpulan yang didapat dari nilai standar deviasi yang didapatkan adalah, kalau nilainya rendah, maka data yang tersedia akan cenderung mendekati nilai rata-rata keseluruhan sampel. Tapi, kalau nilai deviasinya tinggi, data kan menyebar dalam ruang lingkup sampel akan lebih luas ketimbang rata-rata.
Rumus Deviasi
Ada beberapa rumus yang bisa dipakai untuk menentukan deviasi, sesuai dengan jenis yang mau didapatkan.
Rumus Standar Deviasi Tunggal

Seperti terlihat pada gambar, rumus ini dipakai untuk menentukan deviasi pada sekumpulan data kategori sederhana. Ketika data tersebut masih baku dan belum masuk klasifikasi interval.
Rumus Standar Deviasi Kelompok

Anda bisa melihat dengan jelas rumus di atas, dimana nantinya data yang bisa dimasukkan ke dalam rumus ini sudah masuk di dalam klasifikasi interval. Dimana akan dilihat simpangan baku, dengan melibatkan frekuensi dari masing-masing data.
Contoh Soal Simpangan Baku
Untuk bisa menerapkan rumus di atas, maka Anda perlu memahami juga contoh soal berikut ini. Mulai dari yang sederhana, sampai yang sulit. Supaya dapat ditentukan nantinya, mana rumus tepat dipakai sehingga nilai simpangan baku yang didapatkan benar.
Ada sekumpulan data yang ingin dicari standar deviasinya. Data tersebut dalah 4,6,8,9,8,7,6. Berapakah standar deviasi dari data tersebut?
Diketahui: data 4,6,8,9,7,6
Tanya: S?
Jawab: 1. Yang perlu dicari terlebih dahulu adalah nilai rata-rata dari data
= (8+7+8+9+7+9)/6 = 8
- Menghitung varian
= {(8-8)2+(7-8)2+(8-8)2+(9-8)2+(7-8)2+(9-8)2}/6
=(0+1+0+1+0+1)/6
= 3/6 = 0,5
- Mencari Standar Deviasi
= √0,5
= 0,7
Jadi, bisa disimpulkan bahwa nilai simpangan baku dari data di atas adalah 0,7
Contoh Penggunaan Standar Deviasi dalam Kehidupan Sehari-Hari
Dalam berbagai kegiatan sehari-hari hingga dunia bisnis, menentukan simpangan baku adalah salah satu hal penting untuk dilakukan. fungsinya jadi sangat beragam, tergantung untuk apakah nilai itu didapatkan.
Di Bidang Kesehatan
Menentukan nilai deviasi akan sangat dibutuhkan ketika melakukan fase uji coba pada sebuah obat. Sehingga bisa didapatkan sejauh mana obat tersebut efektif digunakan oleh pasien sesuai fungsi yang ingin diterapkan dari obat tersebut.
Di Bidang Properti
Beda lagi dengan bidang properti, salah satunya adalah saat perencanaan pembuatan real estate untuk mengetahui variasi dari harga rumah yang akan dibangun. Kemudian akan disesuaikan dengan wilayah tempat pembangunannya dan luas dari rumah tersebut.
Di Bidang Investasi
Sebelum melakukan sebuah investasi, misalnya saham. Para investor akan sangat membutuhkan nilai simpangan baku ini untuk melihat nilai resiko yang dari emiten pilihan, melalui portofolio yang diberikan. Sehingga nantinya bisa dijadikan acuan untuk menentukan keuntungan potensial bisa didapatkan.
Di Bidang Bisnis
Salah satu yang membutuhkan simpangan baku adalah bisnis logistik, dimana pihak pebisnis bisa memperkirakan waktu yang jelas untuk mengirimkan suatu barang. Bisa berdasarkan lokasi yang dituju, dan faktor lainnya.
Deviasi juga akan sering digunakan jika ingin menentukan sebuah produk berkualitas, ke berbagai daerah. Dengan mencari mana produk terbaik dan daerah mana yang potensial menjadi target pasar.
Bagaimana Jika Standar Deviasi Lewat Batas yang Ada?
Bukan hal yang aneh ketika nilai deviasi yang didapatkan dari sekumpulan data ternyata melewati standar batas tertentu. Jika hal ini terjadi, maka perlu dilakukan beberapa cara untuk memahami kenapa hal itu dapat terjadi.
Menggunakan Diagram Pencar atau Histogram
Dengan memvisualisasikan data menggunakan diagram tersebut, Anda akan melihat lebih jelas pola alur dan distribusi data. Mana data yang melewati batas standar deviasi, kemudian dicarikan solusi untuk meminimalisir data yang lewat batas itu jika memang diperlukan.
Memilih Model Analisis Statistik Kompleks
Ketika nilai simpangan baku sudah didapat dan ternyata melewati ambang batas, maka yang bisa dilakukan adalah memilih jenis analisis statistik yang lebih tepat, apalagi, kalau data yang dimiliki merupakan data kelompok, akan dibutuhkan model analisis statistik yang lebih kompleks.
Gunanya adalah untuk meminimalisir dampak dari nilai yang melewati batas tersebut, supaya tidak mempengaruhi data secara keseluruhan dan output yang ingin dicapai.
Pahami Sebab
Pada kondisi tertentu, dimana data yang melewati simpangan baku memberikan indikasi sebuah ketidakpastian akan dibutuhkan pemahaman lebih maksimal tentang apa penyebabnya. Perlu dilakukan analisa lanjutan, apalagi jika data tersebut sangat penting untuk sebuah proses pengambilan keputusan.
Menghapus Outliers
Outliers atau biasa juga disebut pencilan, bisa saja menjadi bagian dari sebuah data sehingga menyebabkan nilai simpangan baku melewati ambang yang ada. Pencilan yang merupakan nilai ekstrim itu, perlu diperiksa terlebih dahulu, apakah memang benar nilainya atau malah salah saat melakukan identifikasi data awal.
Jika memang salah dan akan mengganggu sebuah proses selanjutnya, maka dengan menggunakan metode tertentu bisa dihapuskan untuk bisa mendapatkan nilai deviasi yang lebih baik.
Keputusan atas Variasi Signifikan
Pada data seperti keuangan, penelitian, hingga performa sebuah produk, bisa jadi muncul variasi data yang signifikan sehingga menjadi penyebab munculnya contoh simpangan baku yang jauh melebihi ambang batas.
Pada kondisi tersebut, bisa dilakukan tindakan lanjutkan dengan mengidentifikasi terlebih dahulu penyebabnya, lalu dicarikan solusi dan keputusan tepat atas variasi yang terjadi.
Karakteristik Nilai Terbaik dari Sebuah Standar Deviasi
Sebenarnya sebuah nilai simpangan baku sangat bervariasi, namun ada beberapa karakteristik yang sering dijadikan acuan untuk menentukan nilai terbaiknya. Sebagai referensi bagi Anda, berikut ini beberapa karakteristiknya.
- Simpangan baku dengan nilai yang lebih besar dibandingkan nilai mean, merupakan indikasi banyaknya variasi dari data yang dihitung
- Simpangan baku dengan nilai yang lebih kecil dibandingkan nilai mean, merupakan indikasi variasi data yang sedikit
- Nilai yang letaknya berada antara -2 sampai +2 bisa dikatakan sudah dapat mewakili semua data yang ada
- Nilai simpangan baku yang tinggi, tidak selalu buruk. Tergantung pada data yang dijadikan objek penentuan nilai tersebut.
- Nilai simpangan baku yang rendah, juga tidak selalu buruk. Ada kalanya nilai rendah justru mampu mewakili dan memberikan hasil yang tepat
Setelah memahami tentang standar deviasi, akan memudahkan Anda untuk mengetahui banyak hal tentang sebuah kelompok data. Karena nilai simpangan baku itu akan membantu pengambilan keputusan hingga berbagai kebutuhan penghitungan penting di berbagai bidang.