Untuk memahami apa itu Chi Square, Anda perlu mengetahui contoh tabel Chi Square yang baik dan benar. Dengan melihat contohnya tersebut, orang-orang bisa lebih memahami pengertian dan karakteristik dari uji non parametrik ini. Maka dari itu, di sini kami akan membagikan contohnya juga.
Umumnya, Chi Square digunakan oleh banyak orang untuk melakukan penelitian, baik yang skala besar maupun kecil. Contoh penelitian yang menggunakan Chi Square adalah mahasiswa yang sedang mengerjakan skripsi dan harus mengolah datanya dengan menggunakan software statistik.
Selain itu, uji Chi Square juga sering digunakan pada penelitian-penelitian besar yang dilakukan oleh banyak ahli. Namun, Chi Square tidak boleh dilakukan dengan rumus dan cara yang salah, karena hal tersebut dapat mempengaruhi hasil dari seluruh penelitian yang telah dilaksanakan.
Apa itu Chi Square?
Pengertian Chi Square sudah pernah disebutkan dalam buku berjudul Pengantar Statistika karya Usman H. dan R. Purnomo Setiady Akbar. Di dalam buku tersebut dikatakan bahwa Chi Square merupakan uji non parametrik yang biasa digunakan untuk mengetahui hubungan 2 variabel nominal.
Nantinya, penelitian untuk mengetahui hubungan 2 variabel nominal ini bisa dilakukan dengan mengukur kekuatan hubungan antara keduanya. Maka dari itu, di awal kami menyebutkan bahwa Chi Square tidak boleh dilakukan dengan cara dan rumus yang salah.
Umumnya, uji non parametrik ini membutuhkan sampel berukuran besar yang kemudian variabelnya dapat ditabulasikan ke dalam kategori-kategori tertentu. Setelah dikategorikan menjadi beberapa bagian, variabel bisa langsung dihitung dengan menggunakan metode statistik Chi Square ini.
Meski jika dilihat sekilas uji non parametrik ini mungkin terlihat mirip dengan jenis uji non parametrik yang lainnya, tapi sebenarnya uji Chi Square memiliki syarat dan karakteristik tersendiri. Jadi, untuk mempelajari tentang hal ini Anda juga perlu memahami tentang kedua hal tersebut.
Syarat dan Karakteristik Uji Chi Square
Setelah mengetahui pengertian Chi Square dan sebelum membahas tentang contoh tabel Chi Square, Anda perlu mencari tahu tentang syarat dan karakteristik dari uji non parametrik yang satu ini. Sebenarnya, untuk syarat umumnya sendiri adalah sampel yang digunakan berukuran besar.
Sementara untuk karakteristik dari uji Chi Square akan membuatnya lebih mudah dikenali dan dibedakan dari jenis-jenis uji non parametrik yang lainnya. Bagi orang-orang yang belum tahu apa syarat dan karakteristik dari uji Chi Square, mereka bisa menyimak penjelasannya di bawah ini:
1. Syarat Uji Chi Square
Uji Chi Square baru bisa dilakukan ketika semua syarat ini sudah terpenuhi dan tidak ada yang tertinggal. Maka dari itu, orang-orang yang hendak melakukan penelitian dengan menggunakan uji Chi Square harus mengetahui beberapa persyaratan tersebut dengan baik, dan di antaranya adalah:
- Tidak boleh ada 1 sel saja yang memiliki frekuensi harapan pada tabel kontingensi 2 x 2. Hal ini juga sering disebut dengan nama expected count (“Fh”) yang jumlahnya kurang dari 5.
- Tidak ada sel yang didukung dengan nilai frekuensi kenyataan atau nama lainnya adalah actual count (F0) yang jumlahnya 0.
- Jumlah sel pada tabel yang ukurannya lebih dari 2 x 2 harus dipastikan memiliki frekuensi harapan yang kurang dari 5 dan tidak boleh melebihi angka 20%.
2. Karakteristik Uji Chi Square
Ketika melihat tabel Chi Square yang ada pada suatu penelitian, karakteristik ini pasti akan terlihat secara jelas. Sebab, semua uji Chi Square yang dilakukan pada suatu penelitian pasti akan memiliki karakteristik yang seperti berikut ini:
- Nilai dari uji Chi Square selalu positif, sehingga tidak ada angka negatif dalam tabel tersebut.
- Uji Chi Square memiliki beberapa distribusi yang di antaranya adalah DK = 1, 2, 3, 4, 5, dan seterusnya.
- Bentuk distribusi Chi Square menjulur positif dan karakteristik ini dapat ditemukan pada seluruh tabel sejenis ini.
Rumus dan Contoh Tabel Chi Square
Sebelum mengetahui tentang contoh dari tabel uji Chi Square yang tepat, penting untuk banyak orang tahu bahwa uji non parametrik ini berguna untuk menguji hubungan maupun pengaruh 2 buah variabel nominal yang ada.
Jadi, orang-orang bisa lebih mengetahui kuatnya hubungan kedua variabel tersebut. Nantinya, uji Chi Square bisa dihitung dengan rumus X2 = ∑(f0 – fe)2 / fe yang X2 sendiri dapat diartikan sebagai nilai chi kuadrat, fe berarti frekuensi yang diharapkan, dan f0 merupakan frekuensi yang diamati.
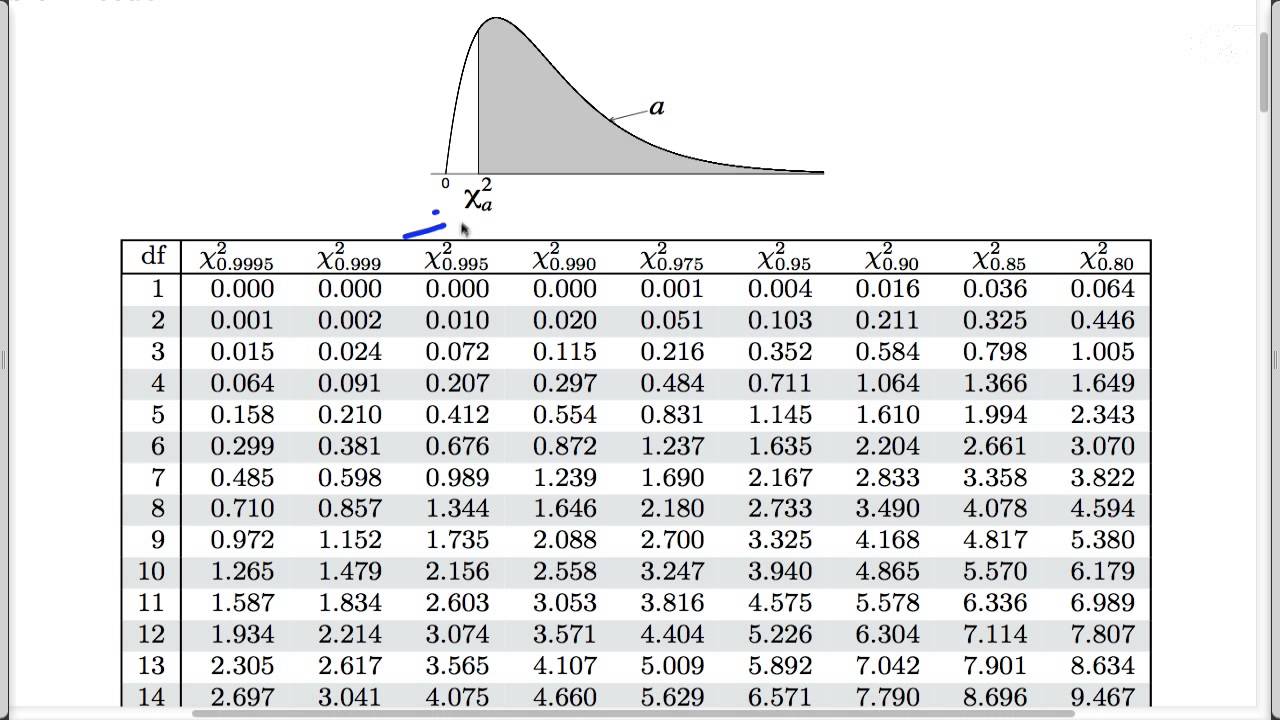
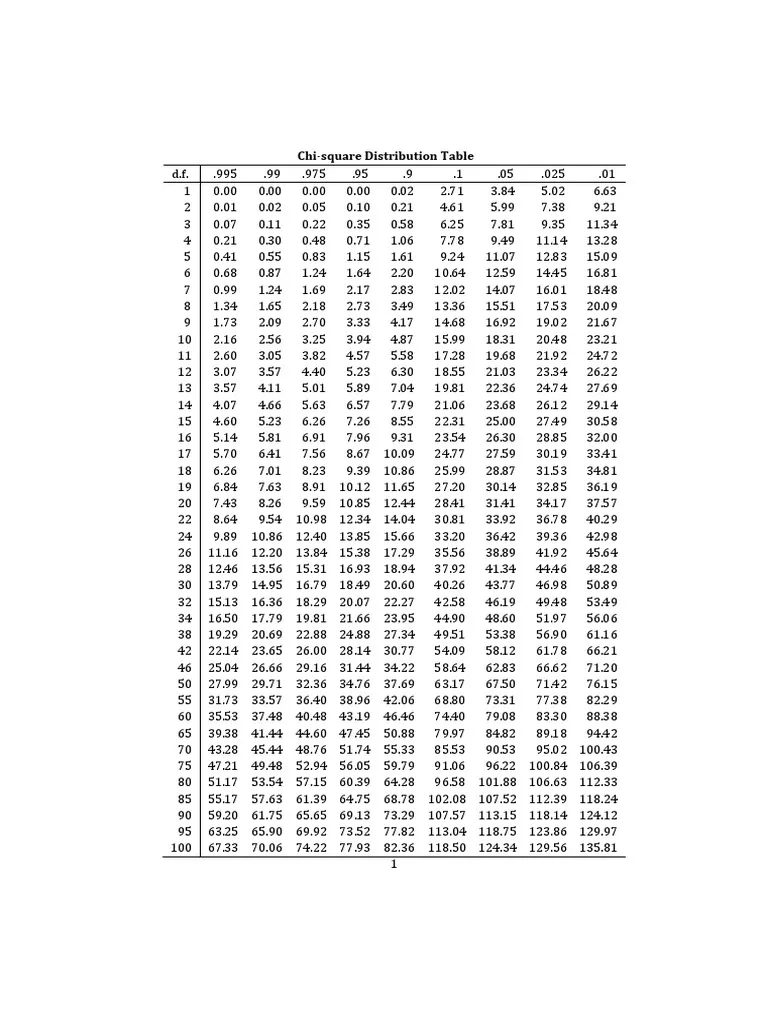
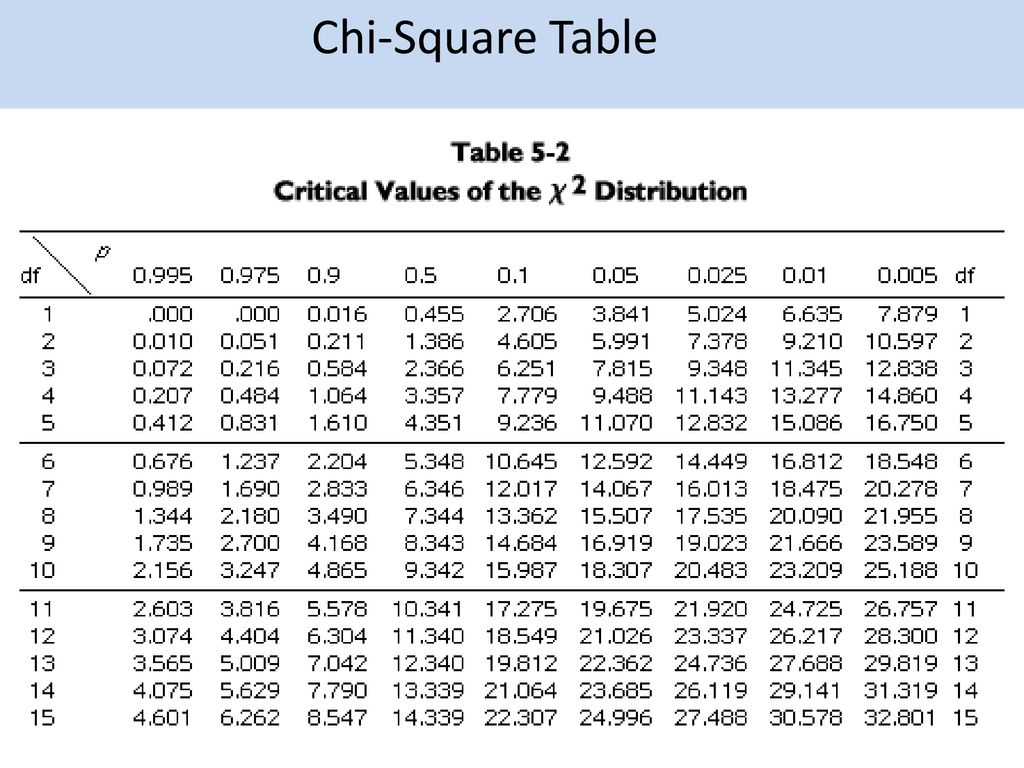
Untuk lebih jelasnya, berikut kami berikan salah satu contoh tabelnya:
| DF | 0,995 | 0,975 | 0,20 | 0,10 | 0,5 | 0,25 | 0,2 | 0,1 |
| 1 | 0,0000393 | 0,000982 | 1,642 | 2,706 | 3,841 | 5,024 | 5,412 | 6,635 |
| 2 | 0,0100 | 0,0506 | 3,219 | 4,605 | 5,991 | 7,378 | 7,824 | 9,210 |
| 3 | 0,0717 | 0,216 | 4,642 | 6,251 | 7,815 | 9,348 | 9,837 | 11,345 |
| 4 | 0,207 | 0,484 | 5,989 | 7,779 | 9,488 | 11,143 | 11,668 | 13,277 |
| 5 | 0,412 | 0,831 | 7,289 | 9,236 | 11,070 | 12,833 | 13,388 | 15,086 |
| 6 | 0,676 | 1,237 | 8,558 | 10,645 | 12,592 | 14,449 | 15,033 | 16,812 |
| 7 | 0,989 | 1,690 | 9,803 | 12,017 | 14,067 | 16,013 | 16,622 | 18,475 |
| 8 | 1,344 | 2,180 | 11,030 | 13,362 | 15,507 | 17,535 | 18,168 | 20,090 |
| 9 | 1,735 | 2,700 | 12,242 | 14,684 | 16,919 | 19,023 | 19,679 | 21,666 |
| 10 | 2,156 | 3,247 | 13,442 | 15,987 | 18,307 | 20,483 | 21,161 | 23,209 |
| 11 | 2,603 | 3,816 | 14,631 | 17,275 | 19,675 | 21,920 | 22,618 | 24,725 |
| 12 | 3,074 | 4,404 | 15,812 | 18,549 | 21,026 | 23,337 | 24,054 | 26,217 |
| 13 | 3,565 | 5,009 | 16,985 | 19,812 | 22,362 | 24,736 | 25,472 | 27,688 |
| 14 | 4,075 | 5,629 | 18,151 | 21,064 | 23,685 | 26,119 | 26,873 | 29,141 |
| 15 | 4,601 | 6,262 | 19,311 | 22,307 | 24,996 | 27,488 | 28,259 | 30,578 |
| 16 | 5,142 | 6,908 | 20,465 | 23,542 | 26,296 | 28,845 | 29,633 | 32,000 |
| 17 | 5,697 | 7,564 | 21,615 | 24,769 | 27,587 | 30,191 | 30,995 | 33,409 |
| 18 | 6,265 | 8,231 | 22,760 | 25,989 | 28,869 | 31,526 | 32,346 | 34,805 |
| 19 | 6,844 | 8,907 | 23,900 | 27,204 | 30,144 | 32,852 | 33,687 | 36,191 |
| 20 | 7,434 | 9,591 | 25,038 | 28,412 | 31,410 | 34,170 | 35,020 | 37,566 |
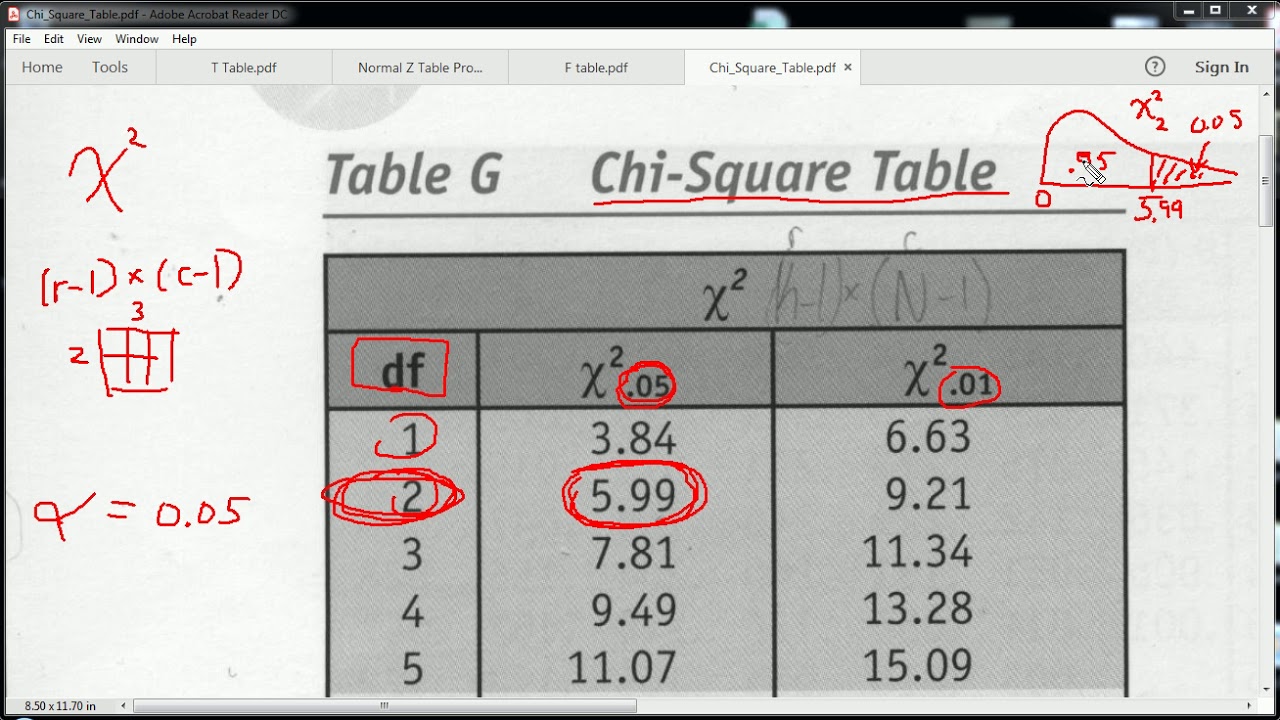
Cara Membaca Tabel Chi Square dengan Mudah
Melihat contoh di atas tanpa mengetahui cara membaca tabelnya dengan benar, maka orang-orang pasti akan merasa kesulitan. Sebab, tidak semua orang tahu bagaimana cara membaca tabel uji Chi Square dengan baik dan benar.
Pada dasarnya, cara membaca tabel uji Chi Square tidak jauh berbeda dengan cara membaca tabel T. Hal ini terjadi karena di dalam tabel uji Chi Square terdapat tingkatan signifikansi (a) dan derajat kebebasan yang dilambangkan dengan DK.
Sebagai contoh, jika nilai a adalah 0,01, maka kemungkinan besar keputusan yang diambil adalah 90% benar.
Derajat kebebasan dari penelitian ini didapatkan dari rumus n-1, sehingga para ahli bisa memiliki observasi yang tepat. Jika obyek yang sedang diteliti bernilai 70, maka derajat kebebasannya adalah:
n – 1 = 70 – 1 = 69
Tabel Chi Square memang tidak semudah itu untuk dipahami oleh banyak orang. Namun, jika Anda sudah tahu bagaimana contoh dan cara membacanya yang benar, maka Anda bisa lebih mudah untuk memahami fungsi dari tabel ini.
Biasanya, tabel uji Chi Square digunakan oleh beberapa ahli untuk melakukan sebuah penelitian pada suatu objek. Jika hasilnya masih berada di angka 0,01, maka hal ini dapat membuktikan bahwa keputusannya benar hingga 90%.