Salah satu bentuk himpunan yang perlu dipelajari adalah diagram venn gabungan ini. Materi seputar diagram venn ini sebenarnya sudah pernah dibahas di SMP tepatnya di kelas 7 tetapi kemungkinan besar Anda sudah lupa dengan pembahasan tersebut.
Hal yang mungkin Anda ingat di dalam materi matematika tersebut mungkin berkaitan dengan gambar lingkaran dimana saling bertumpuk ataupun beririsan. Tidak hanya itu saja, diagram venn sendiri juga dibedakan menjadi beberapa jenis.
Salah satunya adalah berkaitan diagram gabungan dimana juga menjadi materi yang dipelajari dalam pembahasan ini. Untuk memahami informasi tersebut, maka sebaiknya dapat menyimak penjelasan dibawah ini.
Pengertian Diagram Venn
Kendati gambar diagram venn sudah bisa ditemukan dengan mudah di internet, namun Anda mungkin masih bingung dengan pengertiannya. Jadi diagram venn merupakan sebuah diagram yang akan menyajikan data di suatu himpunan dimana menampilkan hubungan antar himpunan itu sesuai dengan kelompok.
Dengan menggunakan jenis diagram tersebut sebenarnya akan memberikan keuntungan tersendiri. Misalnya saja adalah memberikan kemudahan bagi Anda dalam memahami suatu data yang sudah tergabung pada suatu himpunan.
Adapun himpunan yang dimaksud disini dapat berupa kumpulan objek dimana bisa diartikan secara jelas. Sebagai contohnya adalah perlengkapan PC dimana terdiri dari keyboard, CPU, monitor, mouse, speaker dan printer.
Aturan Dalam Membuat Diagram Venn
Apabila Anda ingin membuat diagram ini, maka harus memperhatikan beberapa aturan terlebih dahulu. Aturan inipun wajib untuk diikuti oleh semua orang dan tidak boleh dilewatkan diantaranya adalah sebagai berikut:
- Himpunan lain yang menjadi fokus pembahasan dapat dinyatakan dalam bentuk berupa lingkaran atau kurva tertutup
- Himpunan semesta (s) bisa dinyatakan dalam bentuk persegi panjang. Adapun himpunan semesta ini merupakan semua anggota himpunan yang mana di dalamnya akan memuat himpunan dimana menjadi fokus pembahasan
- Anggota dari setiap himpunan akan dinyatakan di dalam bentuk titik atau noktah
- Apabila terdapat himpunan tidak terhingga, maka setiap anggota tidak perlu lagi dinyatakan sebagai titik.
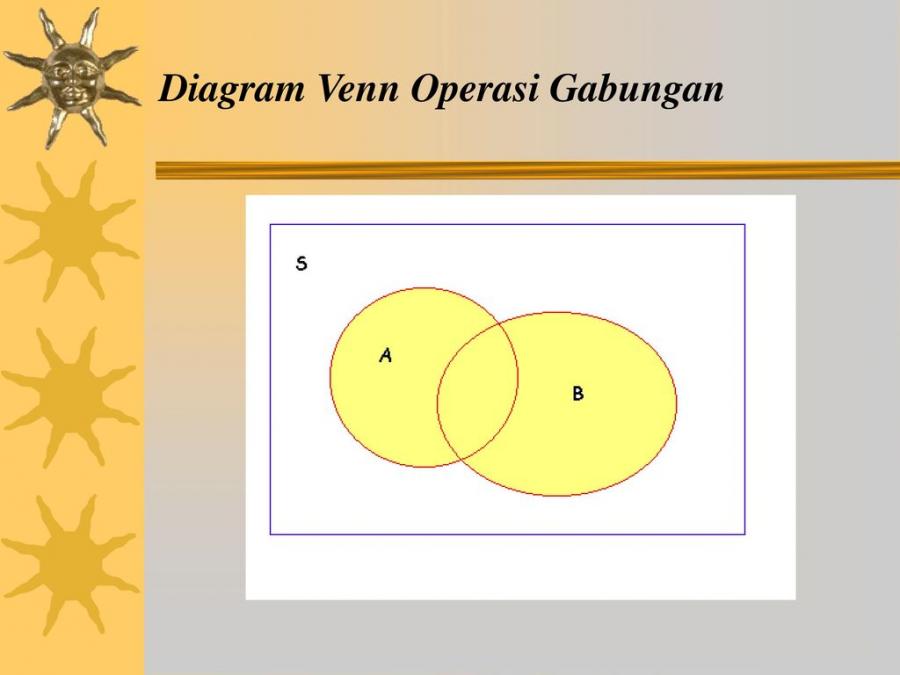
Pengertian Diagram Venn Gabungan
Seperti sudah kami singgung sebelumnya bahwa terdapat beberapa himpunan termasuk diagram venn gabungan ini. Keberadaan dari himpunan tersebut mempunyai kemiripan dengan irisan atau himpunan potongan.
Dimana daerah himpunan A dan B akan diarsir sehingga bisa dikatakan bahwa anggota dari A dan B akan saling berkomunikasi. Adapun jumlah setiap anggota baik himpunan A dan B ditetapkan kombinasinya.
Rumus Himpunan Gabungan
Sudah memahami bagaimana pengertian dari himpunan gabungan diatas? Berikutnya adalah mengenai rumus gabungan ini. Untuk rumus tersebut merupakan hasil kombinasi dan dapat dituliskan berikut ini:
A U B = {x l x ϵ A atau x ϵ B}
Contoh Himpunan Gabungan
Pembahasan berikutnya adalah contoh himpunan gabungan ini dimana kami sudah menyiapkan contoh sederhana agar mudah dipahami oleh para masyarakat.
Terdapat anggota himpunan A ={1, 3, 5, 7, 9,11}
Terdapat anggota himpunan B = {2, 3, 5, 7, 11, 13}
Penyelesaian: pada himpunan gabungan berlaku A U B = {x l x ϵ A atau x ϵ B} sehingga nantinya akan menghasilkan gabungan anggota baru atau kombinasi dari Himpunan A dan B sehingga penulisan penggabungannya adalah A U B: [1, 2, 3, 5, 7, 9, 11, 13} dan berikut contoh diagramnya.
Jenis-jenis Himpunan Lainnya
Selain memahami contoh soal gabungan dari diagram venn di atas, Anda juga perlu memahami jenis jenis himpunan lainnya. Sebab selain himpunan gabungan diatas, beberapa jenis himpunan dibawah ini juga wajib untuk diketahui.
Himpunan Bagian
di dalam himpunan ini maka setiap anggota himpunan A juga termasuk ke dalam himpunan B. Di dalam jenis diagram venn ini akan berlaku A Ո B = B. Sebagai contohnya adalah:
A = {1, 2, 3}
B = {1, 2, 3, 4, 5}
Dari penjelasan di atas maka jelas bahwa semua anggota himpunan A merupakan anggota dari himpunan B juga.
Himpunan Jumlah Sama
Sedangkan himpunan jumlah sama menyatakan bahwa setiap A dan B nantinya akan terdiri dari anggota yang benar benar sama baik dari segi banyaknya angka maupun jenis angka. Kesimpulannya adalah bahwa setiap anggota dari B merupakan anggota A, maka bisa dituliskan A = B.
Himpunan Saling Lepas
Berikutnya adalah himpunan saling lepas dimana berarti setiap anggota A tidak akan saling bergantung dengan pihak anggota B alias tidak sama. Untuk penulisan dari grafisnya adalah A Ո B = [ᴓ}
Himpunan Berpotongan
Ini merupakan jenis diagram dimana menghadirkan dua himpunan yang saling berpotongan sekaligus mempunyai kesamaan dari setiap ataupun beberapa anggotanya. Misalnya saja setiap anggota himpunan A dan B berpotongan, maka dapat diartikan apabila terdapat kesamaan dari data.
Sehingga antara himpunan A dan B dimana saling mempunyai anggota yang berada di dalam potongannya.
Himpunan Komplemen
Jenis berikutnya adalah diagram venn komplemen ini dimana dapat disebut sebagai himpunan tambahan A atau B sehingga bisa ditulis Ac atau Bc. Secara umum juga akan terdapat 1 bagian himpunan saja A atau B.
Jumlah anggota yang terdapat di dalamnya termasuk ke dalam himpunan universal alias S. Untuk memahaminya lebih jauh, maka silahkan simak contohnya di bawah ini:
Anggota S: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
Anggota A: [1, 3, 5, 7, 9]
Penggunaan Diagram Venn Dalam Dunia Matematika
Setelah mengetahui bagaimana cara membaca himpunan gabungan dan penjelasan diatas, maka harus memahami penggunaan diagram di dalam dunia matematika. Di dalam ilmu inilah, kehadiran dari diagram dapat membantu melakukan visualisasi data sehingga bisa lebih mudah dipahami ataupun dianalisa.
Berikut sejumlah penggunaan dari diagram venn baik gabungan ataupun jenis lainnya dalam dunia matematika:
Sebagai Representasi Hubungan Himpunan
Secara umum, keberadaan diagram ini berguna dalam dunia matematika untuk mewakili sekaligus memvisualisasikan hubungan diantara himpunan himpunan. Dengan begitu, akan membantu Anda agar lebih mudah melihat sekaligus memahami elemen yang terdapat di dalam diagram dan bagaimana keterkaitannya.
Menggambarkan Operasi Himpunan
Penggunaan berikutnya adalah untuk menggambarkan operasi himpunan mulai dari irisan, gabungan ataupun selisih. Sebagai contohnya adalah bisa membantu menggambarkan gabungan yang terjadi antara himpunan A dan B.
Membantu Proses Menyelesaikan Soal Matematika
Diagram venn memiliki fungsi buat menyelesaikan soal matematika juga. Sebagai contohnya adalah untuk menyelesaikan soal matematika berkaitan dengan probabilitas, maka diagram venn bisa berfungsi untuk menggambarkan ruang sampel sekaligus perhitungan probabilitasnya dengan baik.
Kehadiran dari diagram venn mungkin bukan menjadi hal asing lagi karena memang sudah dipelajari semenjak SMP. Dari beberapa jenis diagram yang ada, maka diagram gabungan adalah salah satu dimana perlu diketahui.
Diagram gabungan sendiri mempunyai kemiripan dengan himpunan irisan dan berpotongan karena anggota A dan B saling dikombinasikan. Selain diagram venn gabungan, masih terdapat beberapa jenis himpunan lainnya.