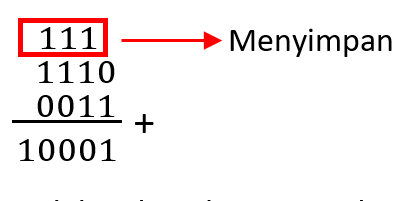Melakukan perhitungan aritmatika pada sistem bilangan tidak semudah menghitung aritmatika pada bilangan biasa. Oleh karena itu kami menulis artikel ini untuk memfasilitasi ruang belajar Anda, pada artikel ini akan membahas bagaimana cara menghitung penjumlahan dan pengurangan sistem bilangan yaitu biner, desimal, oktal, dan heksadesimal.
Cara Menghitung Penjumlahan
A. Penjumlahan pada Sistem Bilangan Biner
Untuk menghitung bilangan biner, Anda perlu memahami konsepnya lebih dahulu. Tetapi jika Anda ingin mempunyai alternatif lain, maka bisa memilih cara dengan merubah bilangan biner menjadi desimal lalu melakukan perhitungan dan kemudian mengkonversinya lagi menjadi biner. Menurut kami alternatif ini cukup rumit dan kurang efisien, untuk itu perlu Anda ketahui konsep berikut:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 1 = 0 menyimpan 1
- 1 + 1 + 1 = 1 menyimpan 1
Contoh soal: hitunglah penjumlahan bilangan biner 1110(2) + 0011(2)?
Jadi hasil perhitungan dari 1110(2) + 0011(2) = 10001(2)
B. Penjumlahan pada Sistem Bilangan Desimal
Untuk melakukan penjumlahan pada sistem bilangan desimal bisa dilakukan seperti penjumlahan pada umumnya. contoh penjumlahan sistem bilangan desimal adalah sebagai berikut:
Berapakah jumlah dari 250(10) + 123(10)?
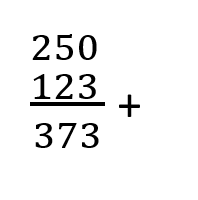
C. Penjumlahan pada Sistem Bilangan Oktal
Untuk melakukan operasi penjumlahan pada bilangan oktal, ada konsep yang harus Anda pelajari. Karena didalam bilangan oktal hanya ada 8 angka yaitu: 0,1,2,3,4,5,6 dan 7. Maka saat ada penjumlahan dalam bilangan desimal hasilnya 8 maka dalam oktal hasilnya adalah 10, saat bilangan desimal hasilnya 9 maka pada bilangan oktal adalah 11, dst. Untuk itu coba perhatikan poin penting ini:
- 0 + 0 = 0
- 0 + 1 = 1
- 0 + 2 = 2
- 0 + 3 = 3
- 0 + 4 = 4
- 0 + 5 = 5
- 0 + 6 = 6
- 0 + 7 = 7
- 1 + 1 = 2
- 1 + 2 = 3
- 1 + 3 = 4
- 1 + 4 = 5
- 1 + 5 = 6
- 1 + 6 = 7
- 1 + 7 = 10
- 2 + 6 = 10
- 2 + 7 = 11
- 2 + 8 = 12
- 3 + 5 = 10
- 4 + 5 = 11
- 4 + 6 =12
- Dst
Dengan mengetahui dasar konsep di atas, maka cara melakukan penjumlahan bilangan oktal sama saja seperti bilangan desimal. Perhatikan contoh berikut:
Hitunglah penjumlahan bilangan oktal 123(8) + 47(8)?
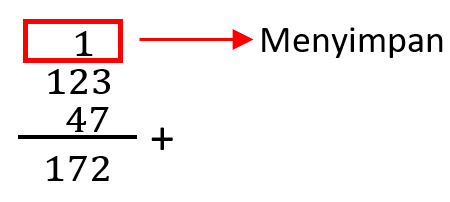
Jadi hasil perhitungan dari 123(8) + 47(8) = 172
D. Penjumlahan pada Sistem Bilangan Heksadesimal
Penjumlahan pada bilangan heksadesimal sama dengan penjumlahan pada desimal dan oktal, hanya saja ketika terjadi penyimpanan “1” maka nilainya adalah 16. Jika penjumlahan yang dilakukan nilainya lebih dari 15 akan terjadi penyimpanan 1, dan kemudian hasil penjumlahan dikurangi dengan 16 yang nantinya akan jadi hasil dari penjumlahan desimal. Perhatikan contoh berikut ini:
1A8(16) + D89(16) = …. (16)
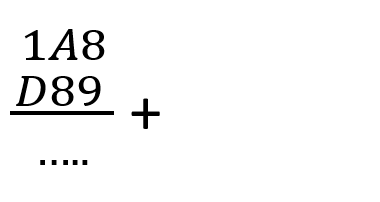
Untuk menyelesaikan soal ini tahapnya adalah berikut:
- 8 + 7 = 17 karena lebih dari 15 maka menyimpan 1 dan hasil penjumlahannya heksadesimalnya adalah 17-16=
- 1 + A + 8, angka 1 diperoleh dari simpanan hasil penjumlahan sebelumnya. A=10 pada bilangan desimal, jadi 1 + 10 + 8 = 19, karena lebih dari 15 maka menyimpan 1 dan hasil penjumlahannya adalah 3 dari perhitungan 19-16.
- 1 + 1 + D = 1 + 1 + 13 = 15, maka hasil penjumlahannya adalah
- Maka hasil penjumlahan adalah bilangan yang diwarnai merah, jadi 1A8(16) + D89(16) = F31(16)
Cara Menghitung Pengurangan
A. Pengurangan pada Sistem Bilangan Biner
Melakukan pengurangan pada sistem bilangan biner, Anda harus memahami konsep perhitungan pada sistem bilangan desimal atau biasa. Ketika Anda melakukan pengurangan pada digit desimal dengan digit yang lebih kecil maka akan ada konsep peminjaman, digit yang kurang akan meminjam 1 dari digit di sebelah kirinya. Perhatikan konsep penting ini:
- 0 – 0 = 0
- 1 – 0 = 1
- 1 – 1 = 0
- 0 – 1 = 1 memijam “1” dari digit sebelahnya
Contoh soalnya: hitunglah pengurangan 11011(2) – 1100(2) ?
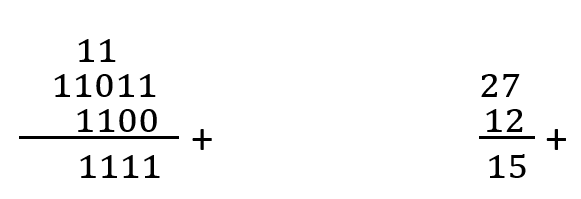
Jadi hasil perhitungan dari 11011(2) + 1100(2) = 1111(2)
B. Pengurangan pada Sistem Bilangan Desimal
Untuk melakukan pengurangan pada bilangan desimal sama seperti melakukan operasi pengurangan pada bilangan pada umumnya.
C. Pengurangan pada Sistem Bilangan Oktal
Untuk melakukan operasi pengurangan pada bilangan oktal caranya sama dengan bilangan desimal, hanya saja perbedaan terletak ketika pengurangan membutuhkan angka simpanan maka jika pada bilangan desimal adalah 10, maka angka simpanan pada bilangan oktal adalah 8. Untuk itu perhatikan contoh berikut:
Berapakah 125(8) – 68(8) dan 1235(8) – 678(8)?
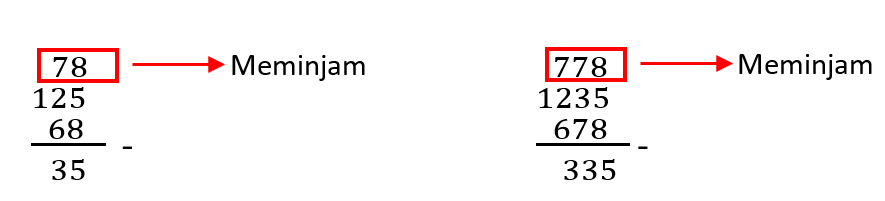Jadi hasil dari 125(8) – 68(8) = 35(8) dan 1235(8) – 678(8) = 335(8)
D. Pengurangan pada Sistem Bilangan Heksadesimal
Untuk pengurangan pada heksadesimal caranya sama dengan pengurangan pada bilangan desimal dan oktal, yang membedakan adalah saat proses perhitungan dan memerlukan angka pinjaman maka bilangan heksadesimal akan bernilai 16 (F), sedangkan desimal adalah 10, dan oktal adalah 8. Perhatikan contoh soal berikut:
Berapakah hasil dari E31(16) – B89(16)?
Untuk menyelesaikan soal ini tahapnya adalah:
- 1 – 9. karena 1 lebih kecil dari 9, maka akan terjadi peminjaman 1 yang bernilai 16. Sehingga angka pertama menjadi 1 + 16 = 17, lalu hasil pengurangan heksa desimalnya adalah 17 – 9 = 8.
- 2 – 8, karena terjadi peminjaman pada perhitungan sebelumnya maka angka 3 – 1 = 2. Lalu karena 2 lebih kecil dari 8 maka akan terjadi peminjaman lagi, sehingga menjadi 2 + 16 = 18. Hasil heksadesimal dari perhitungan ini adalah 18 – 8 = 10 (A).
- D – B = 13 – 11 = 2. Kenapa menjadi D? karena sebelumnya sudah dipinjam sehingga E – 1 = D.
- Hasil perhitungan adalah angka yang berwarna merah, E31(16) – B89(16) = 2A8(16).